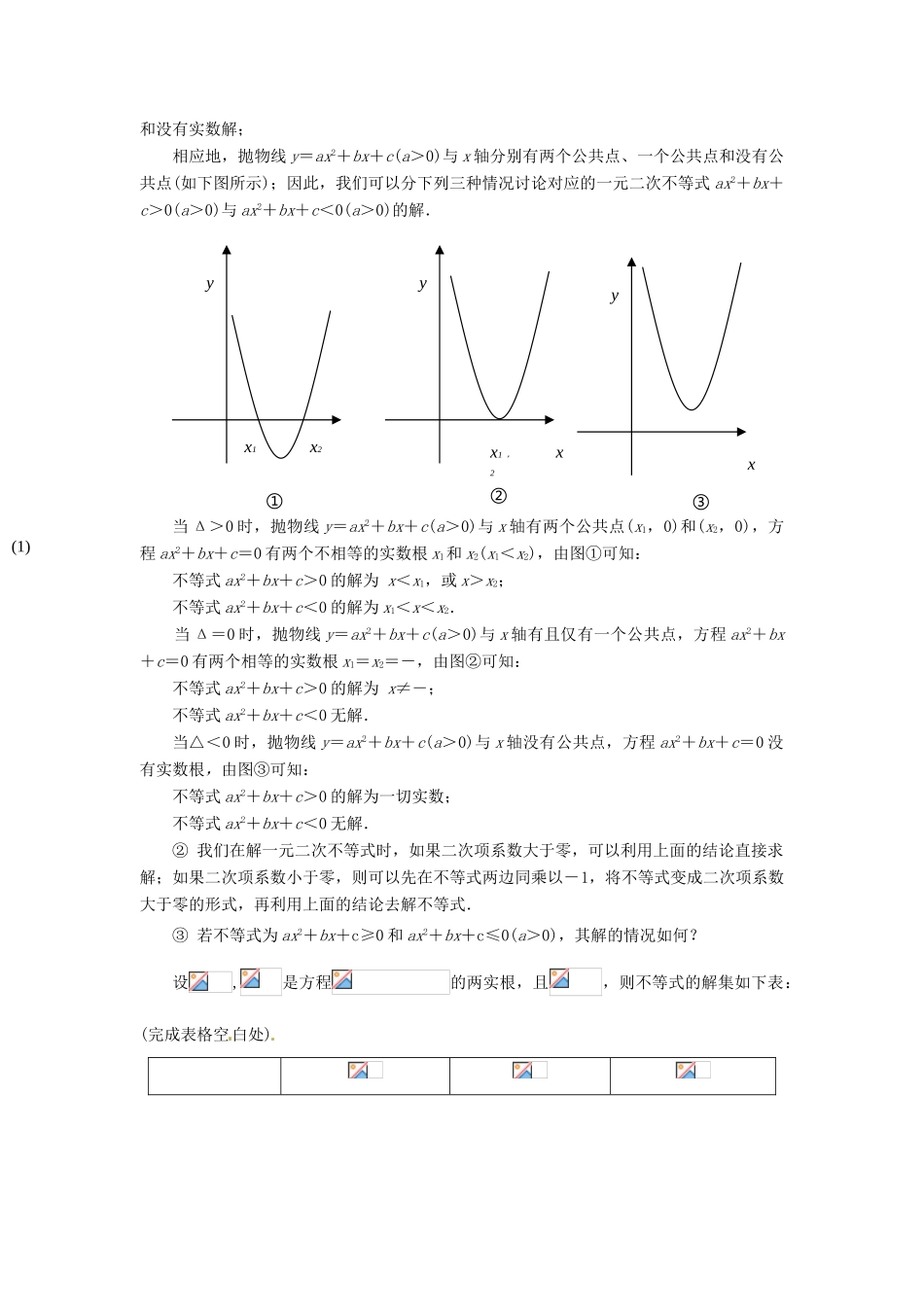
一元二次不等式一、 学习内容、要求及建议知识、方法要求建议解一元二次不等式类比掌握类比一次函数、一元一次不等式、一元一次方程之间的关系,通过一元二次方程的解、二次函数的图像探求一元二次不等式的解法,熟悉三个二次型的相互转换.一元二次方程、二次函数、一元二次不等式的联系数形结合理解二、 预习指导1. 预习目标(1)回顾一次函数、一元一次不等式、一元一次方程之间的关系;(2)探究一元二次不等式的解法.2. 预习提纲(1) 复习一次函数、一元一次方程,一元一次不等式三者关系 完成下表空白处一次函数的图象一元一次方程的解一元一次不等式的解一元一次不等式的解一次函数、一元一次方程、一元一次不等式三者关系是:一次函数所表示的直线与 x轴的交点的横坐标是对应的一元一次方程的根,直线在 x 轴上方(或下方)的点的横坐标的取值范围就是一元一次不等式的解.(2) 类比探究“一次函数、一元一次方程、一元一次不等式”三者之间的关系的做法,我们可以从一元二次方程的解、二次函数的图像探求一元二次不等式的解法.① 对于一元二次方程 ax2+bx+c=0(a>0),设△=b2-4ac,它的解的情形按照△>0,△=0,△<0 分别为下列三种情况——有两个不相等的实数解、有两个相等的实数解xyy=ax+bOxyy=ax+bO和没有实数解;相应地,抛物线 y=ax2+bx+c(a>0)与 x 轴分别有两个公共点、一个公共点和没有公共点(如下图所示);因此,我们可以分下列三种情况讨论对应的一元二次不等式 ax2+bx+c>0(a>0)与 ax2+bx+c<0(a>0)的解.当 Δ>0 时,抛物线 y=ax2+bx+c(a>0)与 x 轴有两个公共点(x1,0)和(x2,0),方程 ax2+bx+c=0 有两个不相等的实数根 x1和 x2(x1<x2),由图①可知:不等式 ax2+bx+c>0 的解为 x<x1,或 x>x2; 不等式 ax2+bx+c<0 的解为 x1<x<x2. 当 Δ=0 时,抛物线 y=ax2+bx+c(a>0)与 x 轴有且仅有一个公共点,方程 ax2+bx+c=0 有两个相等的实数根 x1=x2=-,由图②可知:不等式 ax2+bx+c>0 的解为 x≠-; 不等式 ax2+bx+c<0 无解.当△<0 时,抛物线 y=ax2+bx+c(a>0)与 x 轴没有公共点,方程 ax2+bx+c=0 没有实数根,由图③可知:不等式 ax2+bx+c>0 的解为一切实数;不等式 ax2+bx+c<0 无解.② 我们在解一元二次不等式时,如果二次项系数大于零,可以利用上面的结论直接求解;如果二次项系数小于零,则...