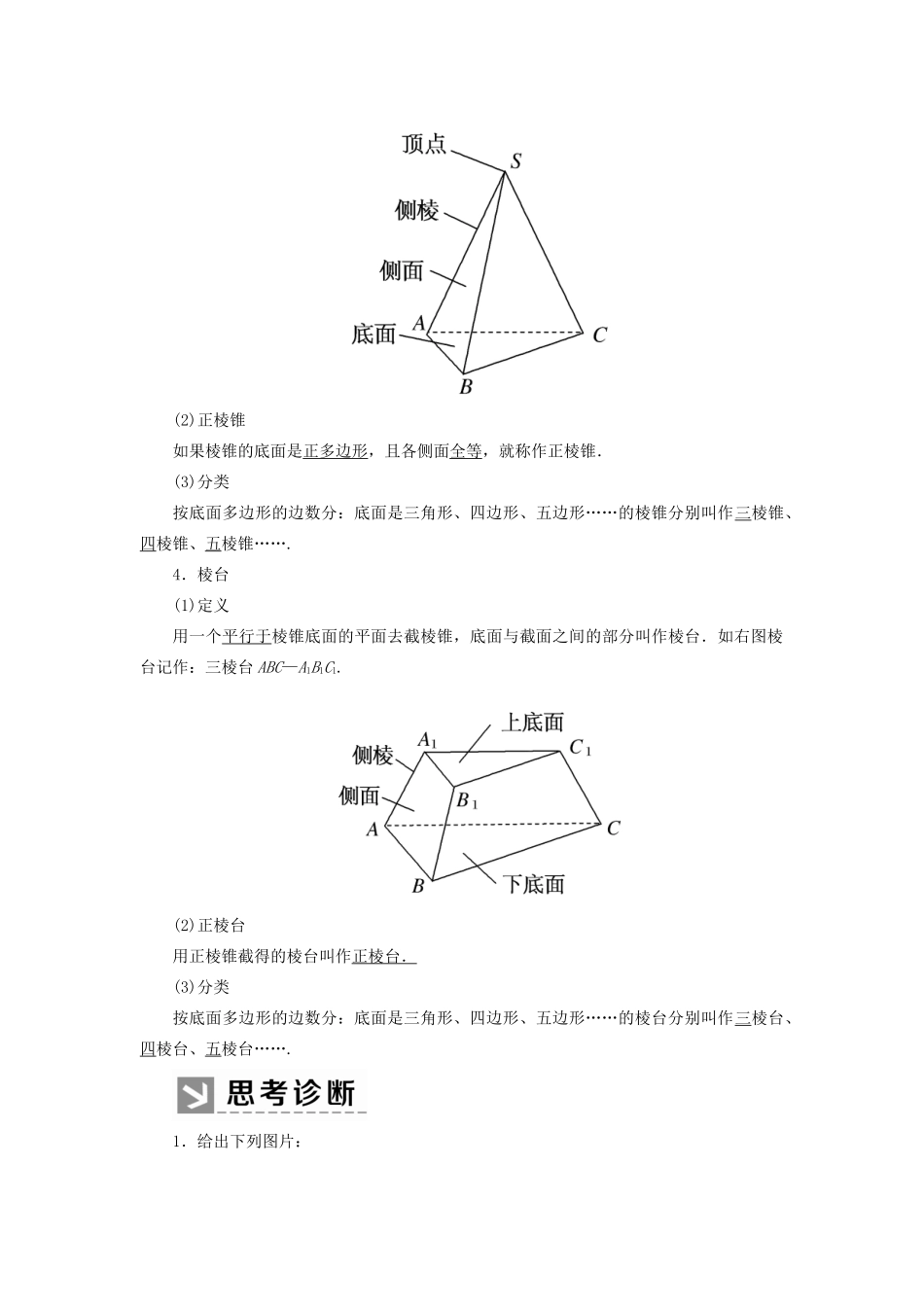
1.2 简单多面体1.多面体我们把若干个平面多边形围成的几何体叫作多面体.其中棱柱、棱锥、棱台都是简单多面体.2.棱柱(1)棱柱的有关概念两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫作棱柱.两个互相平行的面叫作棱柱的底面,其余各面叫作棱柱的侧面,棱柱的侧面是平行四边形.两个面的公共边叫作棱柱的棱,其中两个侧面的公共边叫作棱柱的侧棱,底面多边形与侧面的公共顶点叫作棱柱的顶点.(2)棱柱的分类① 按底面多边形的边数:棱柱的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫作三棱柱、四棱柱、五棱柱…….② 按侧棱与底面是否垂直:3.棱锥(1)定义有一个面是多边形,其余各面是有一个公共顶点的三角形,这些面围成的几何体叫作棱锥.如右图棱锥记作:三棱锥 S—ABC.(2)正棱锥如果棱锥的底面是正多边形,且各侧面全等,就称作正棱锥.(3)分类按底面多边形的边数分:底面是三角形、四边形、五边形……的棱锥分别叫作三棱锥、四棱锥、五棱锥…….4.棱台(1)定义用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台.如右图棱台记作:三棱台 ABC—A1B1C1.(2)正棱台用正棱锥截得的棱台叫作正棱台.(3)分类按底面多边形的边数分:底面是三角形、四边形、五边形……的棱台分别叫作三棱台、四棱台、五棱台…….1.给出下列图片:观察这些图片中的物体,你能得到什么样的空间几何体?请与下面轮廓图对应,并将它们进行分类.[答案] 图片中展示的几何体有:柱体、锥体、台体、球体四类. 可作两种不同的分类:2.正棱锥的侧面是什么样的三角形?正棱台的侧面呢?[答案] 正棱锥的侧面是全等的等腰三角形;正棱台的侧面是全等的等腰梯形.3.判断正误(正确的打“√”,错误的打“×”)(1)棱柱的侧面都是平行四边形.( )(2)棱锥的侧面为三角形,且所有侧面都有一个公共点.( )(3)棱台的侧面有的是平行四边形,有的是梯形.( )(4)棱台的侧棱所在直线均相交于同一点.( )(5)多面体至少有四个面.( )(6)三棱锥也叫作四面体.( )[答案] (1)√ (2)√ (3)× (4)√ (5)√ (6)√题型一棱柱的几何特征【典例 1】 如图所示的直八棱柱,它的底面边长都是 5 厘米,侧棱长都是 6 厘米,回答下列问题:(1)这个八棱柱一共有多少面?它们的形状分别是什么图形?哪些面的形状、面积完全相同?(2)这个八棱柱一共有多少条棱?它们的长度分别是多少?(3)...