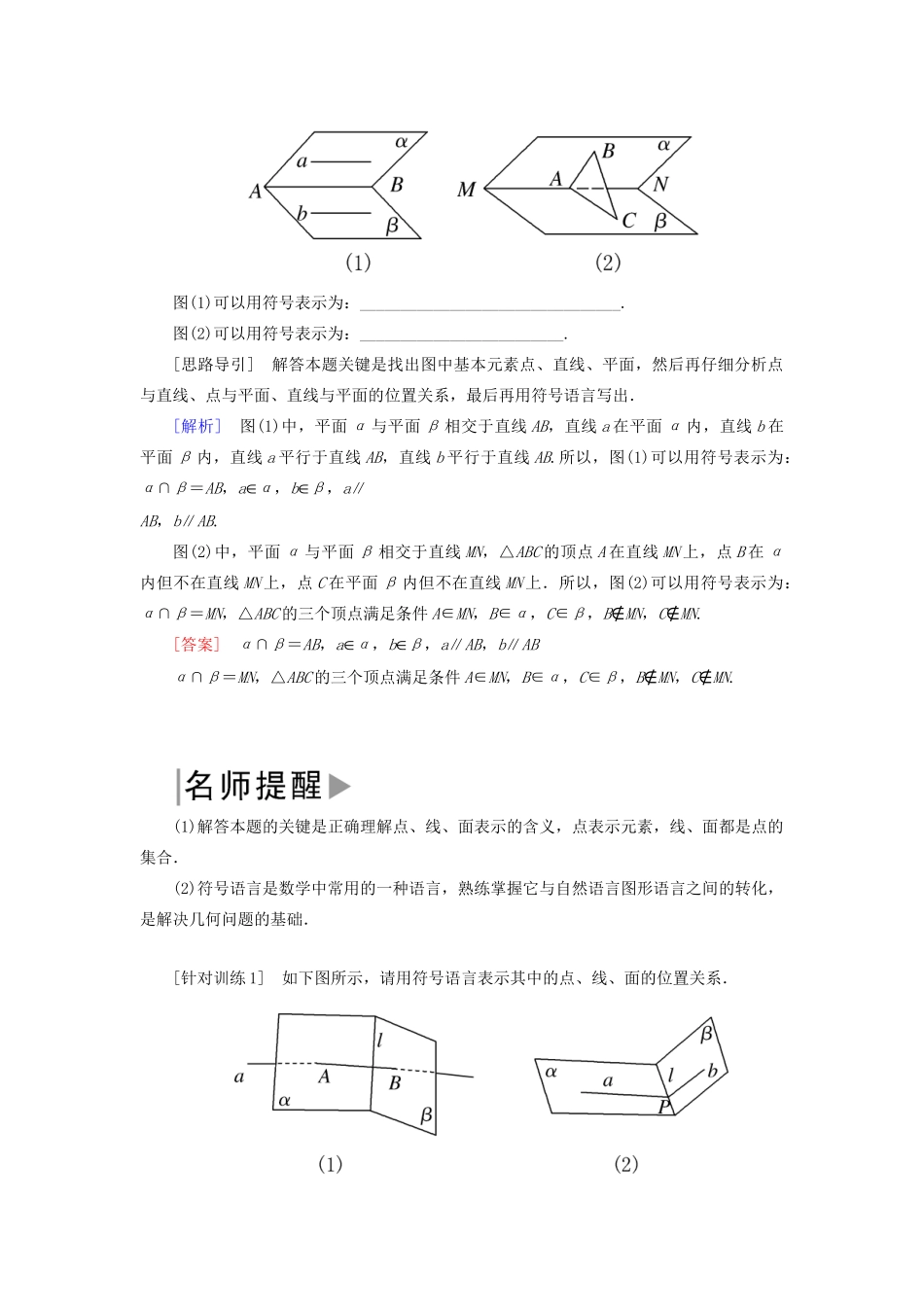
4.1 空间图形基本关系的认识 4.2 空间图形的公理(第 1课时)1.空间图形的基本关系(1)空间点与直线的位置关系有两种:点在直线上和点在直线外.(2)空间点与平面的位置关系有两种:点在平面内和点在平面外.2.空间图形的公理(1)公理 1 过不在同一条直线上的三点,有且只有一个平面(即可以确定一个平面).推论 1:一条直线和直线外一点确定一个平面.推论 2:两条相交直线确定一个平面.推论 3:两条平行直线确定一个平面.(2)公理 2 如果一条直线上的两点在一个平面内,那么这条直线在此平面内(即直线在平面内).(3)公理 3 如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线. 判断正误(正确的打“√”,错误的打“×”)(1)直线 l 在平面 α 内,可以记作:l∈α.( )(2)点 A 在平面 α 外,可以记作:A∉α.( )(3)三点确定一个平面.( )(4)由公理 3 可知,两个不重合平面有两种位置关系:相交或平行.( )(5)直线与平面的位置关系有三种:直线在平面内,直线与平面相交,直线与平面平行.( )[答案] (1)× (2)√ (3)× (4)√ (5)√题型一用符号语言表示点、线、面之间的位置关系【典例 1】 如下图所示,写出图形中的点、直线和平面之间的关系.图(1)可以用符号表示为:________________________________.图(2)可以用符号表示为:_________________________.[思路导引] 解答本题关键是找出图中基本元素点、直线、平面,然后再仔细分析点与直线、点与平面、直线与平面的位置关系,最后再用符号语言写出.[解析] 图(1)中,平面 α 与平面 β 相交于直线 AB,直线 a 在平面 α 内,直线 b 在平面 β 内,直线 a 平行于直线 AB,直线 b 平行于直线 AB.所以,图(1)可以用符号表示为:α∩β=AB,aα,bβ,a∥AB,b∥AB.图(2)中,平面 α 与平面 β 相交于直线 MN,△ABC 的顶点 A 在直线 MN 上,点 B 在 α内但不在直线 MN 上,点 C 在平面 β 内但不在直线 MN 上.所以,图(2)可以用符号表示为:α∩β=MN,△ABC 的三个顶点满足条件 A∈MN,B∈α,C∈β,B∉MN,C∉MN.[答案] α∩β=AB,aα,bβ,a∥AB,b∥ABα∩β=MN,△ABC 的三个顶点满足条件 A∈MN,B∈α,C∈β,B∉MN,C∉MN.(1)解答本题的关键是正确理解点、线、面表示的含义,点表示元素,线、面都是点的集合.(2)符号语言是数学中常用的一种语言,熟练掌握它与...