高中数学 第1章 立体几何初步 1-5-2-1 直线与平面平行的性质学案 北师大版必修2-北师大版高一必修2数学学案

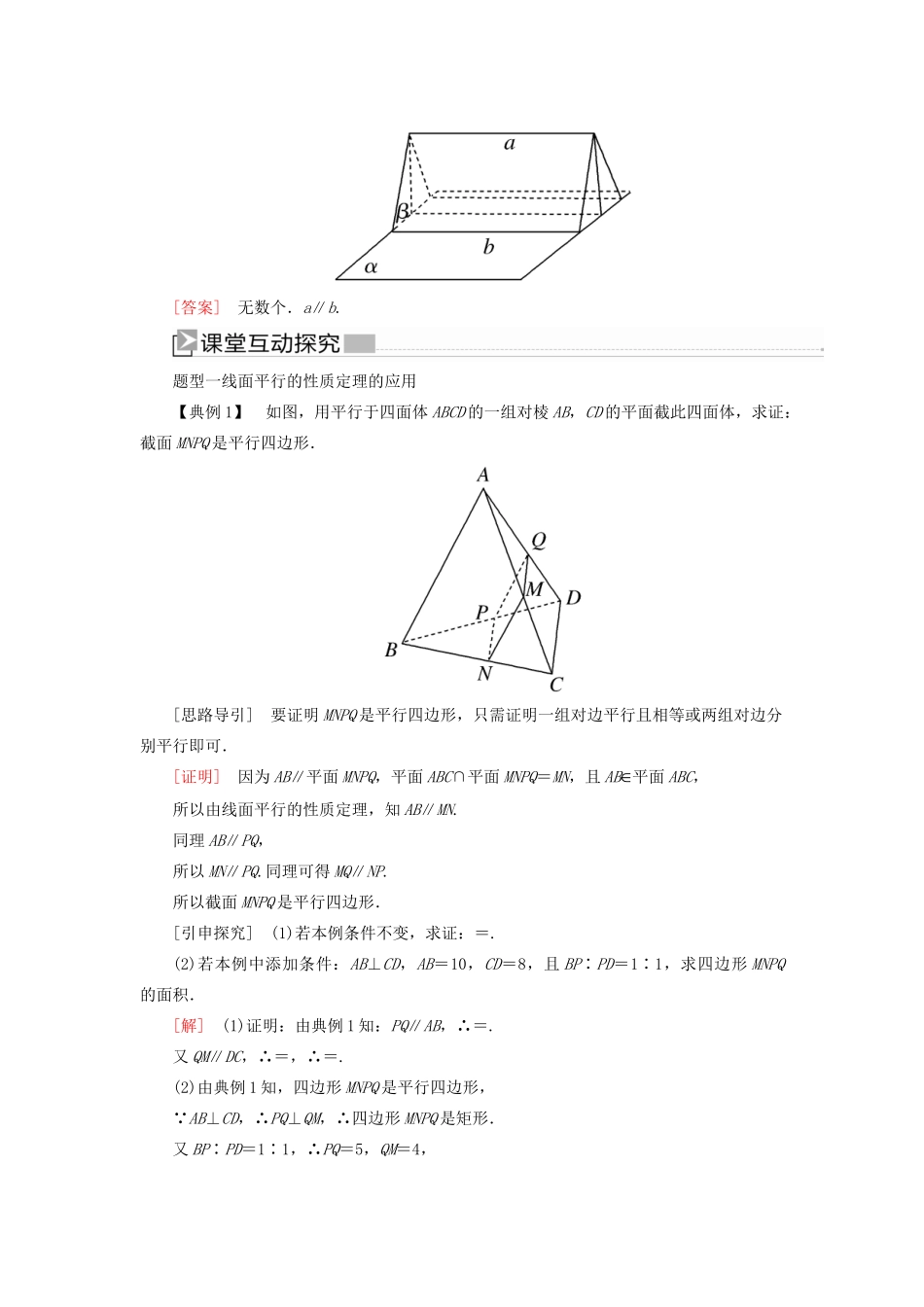
一 直线与平面平行的性质直线和平面平行的性质定理1．如图，直线 l∥平面 α，直线 a平面 α，直线 l 与直线 a 一定平行吗？为什么？[答案] 不一定，因为还可能是异面直线．2．如图，直线 a∥平面 α，直线 a平面 β，平面 α∩平面 β＝直线 b，满足以上条件的平面 β 有多少个？直线 a，b 有什么位置关系？[答案] 无数个．a∥b.题型一线面平行的性质定理的应用【典例 1】 如图，用平行于四面体 ABCD 的一组对棱 AB，CD 的平面截此四面体，求证：截面 MNPQ 是平行四边形．[思路导引] 要证明 MNPQ 是平行四边形，只需证明一组对边平行且相等或两组对边分别平行即可．[证明] 因为 AB∥平面 MNPQ，平面 ABC∩平面 MNPQ＝MN，且 AB平面 ABC，所以由线面平行的性质定理，知 AB∥MN.同理 AB∥PQ，所以 MN∥PQ.同理可得 MQ∥NP.所以截面 MNPQ 是平行四边形．[引申探究] (1)若本例条件不变，求证：＝.(2)若本例中添加条件：AB⊥CD，AB＝10，CD＝8，且 BP∶PD＝1∶1，求四边形 MNPQ的面积．[解] (1)证明：由典例 1 知：PQ∥AB，∴＝.又 QM∥DC，∴＝，∴＝.(2)由典例 1 知，四边形 MNPQ 是平行四边形， AB⊥CD，∴PQ⊥QM，∴四边形 MNPQ 是矩形．又 BP∶PD＝1∶1，∴PQ＝5，QM＝4，∴四边形 MNPQ 的面积为 5×4＝20.运用线面平行的性质定理时，应先确定线面平行，再寻找过已知直线的平面与平面相交的直线，然后确定线线平行，证题过程应认真领悟线线平行与线面平行的相互关系．[针对训练 1] 如图，正方体 ABCD－A1B1C1D1中，AB＝2，点 E 为 AD 的中点，点 F 在 CD上，若 EF∥平面 AB1C，则线段 EF 的长度等于________．[解析] EF∥平面 AB1C，又平面 ADC∩平面 AB1C＝AC，EF平面 ADC，∴EF∥AC， E 是 AD 的中点，∴EF＝AC＝×2＝.[答案] 题型二线面平行性质定理与判定定理的综合应用【典例 2】 求证：如果一条直线和两个相交平面都平行，那么这条直线和它们的交线平行．[思路导引] 利用线面平行的性质定理在面中找到与线平行的直线，然后利用平行公理 4，证明线线平行．[证明] 已知直线 a、l，平面 α、β 满足 α∩β＝l，a∥α，a∥β.求证：a∥l.如图所示，过 a 作平面 γ 交平面 α 于 b， a∥α，∴a∥b.同样过 a 作平面 δ 交平面 β 于 c， a∥β，∴a∥c.则 b∥c.又 bβ，cβ，∴b∥β.又 bα，α∩β＝l，...