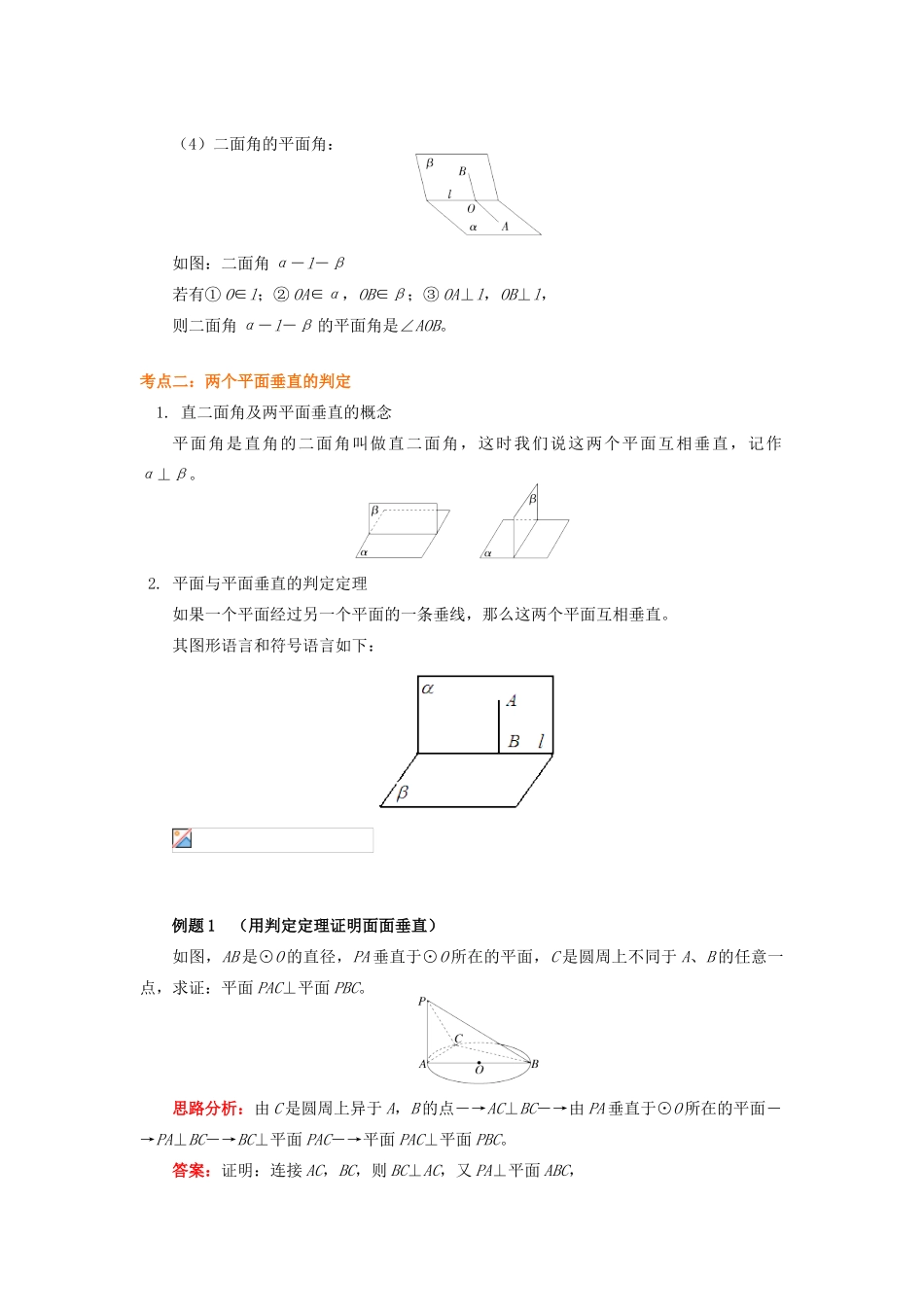
面面垂直的判定一、考点突破知识点课标要求题型说明面面垂直的判定1. 理解二面角及其平面角的概念,能确认图形中的已知角是否为二面角的平面角;2. 掌握二面角的平面角的一般作法,会求简单的二面角的平面角;3. 掌握两个平面互相垂直的概念,能用定义和定理判定面面垂直。选择题填空题解答题面面垂直的定义及判定定理,是前面知识的巩固升华,又是后面研究线面、面面垂直性质的基础。所以,本节课的内容及思想方法,在整个立体几何里,有非常重要的作用。二、重难点提示重点:平面和平面垂直的判定。难点:二面角的理解及度量。考点一:二面角1. 半平面平面内的一条直线把这个平面分成两部分,其中的每一部分都叫做半平面。2. 二面角(1)定义:一条直线和由这条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面。(2)画法:直立式 平卧式(3)记法:二面角 α-l-β 或 α-AB-β 或 P-l-Q 或 P-AB-Q.(4)二面角的平面角:如图:二面角 α-l-β若有① O∈l;② OA∈α,OB∈β;③ OA⊥l,OB⊥l,则二面角 α-l-β 的平面角是∠AOB。考点二:两个平面垂直的判定1. 直二面角及两平面垂直的概念平面角是直角的二面角叫做直二面角,这时我们说这两个平面互相垂直,记作α⊥β。2. 平面与平面垂直的判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。其图形语言和符号语言如下: 例题 1 (用判定定理证明面面垂直)如图,AB 是⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是圆周上不同于 A、B 的任意一点,求证:平面 PAC⊥平面 PBC。思路分析:由 C 是圆周上异于 A,B 的点―→AC⊥BC―→由 PA 垂直于⊙O 所在的平面―→PA⊥BC―→BC⊥平面 PAC―→平面 PAC⊥平面 PBC。答案:证明:连接 AC,BC,则 BC⊥AC,又 PA⊥平面 ABC,∴PA⊥BC,而 PA∩AC=A,∴BC⊥平面 PAC,又 BC⊂平面 PBC,∴平面 PAC⊥面 PBC。技巧点拨:证明面面垂直的方法有:面面垂直的定义和面面垂直的判定定理,而本题二面角 A—PC—B 的平面角不好找,故用判定定理,而用判定定理证面面垂直的关键是在其中一个平面内找(作)一条直线与另一个平面垂直。例题 2 (用定义法求二面角) 如图,已知四边形 ABCD 是正方形,PA⊥平面 ABCD。(1)求二面角 B-PA-D 平面角的度数;(2)求二面角 B-PA-C 平面角的度数。思路分析:...