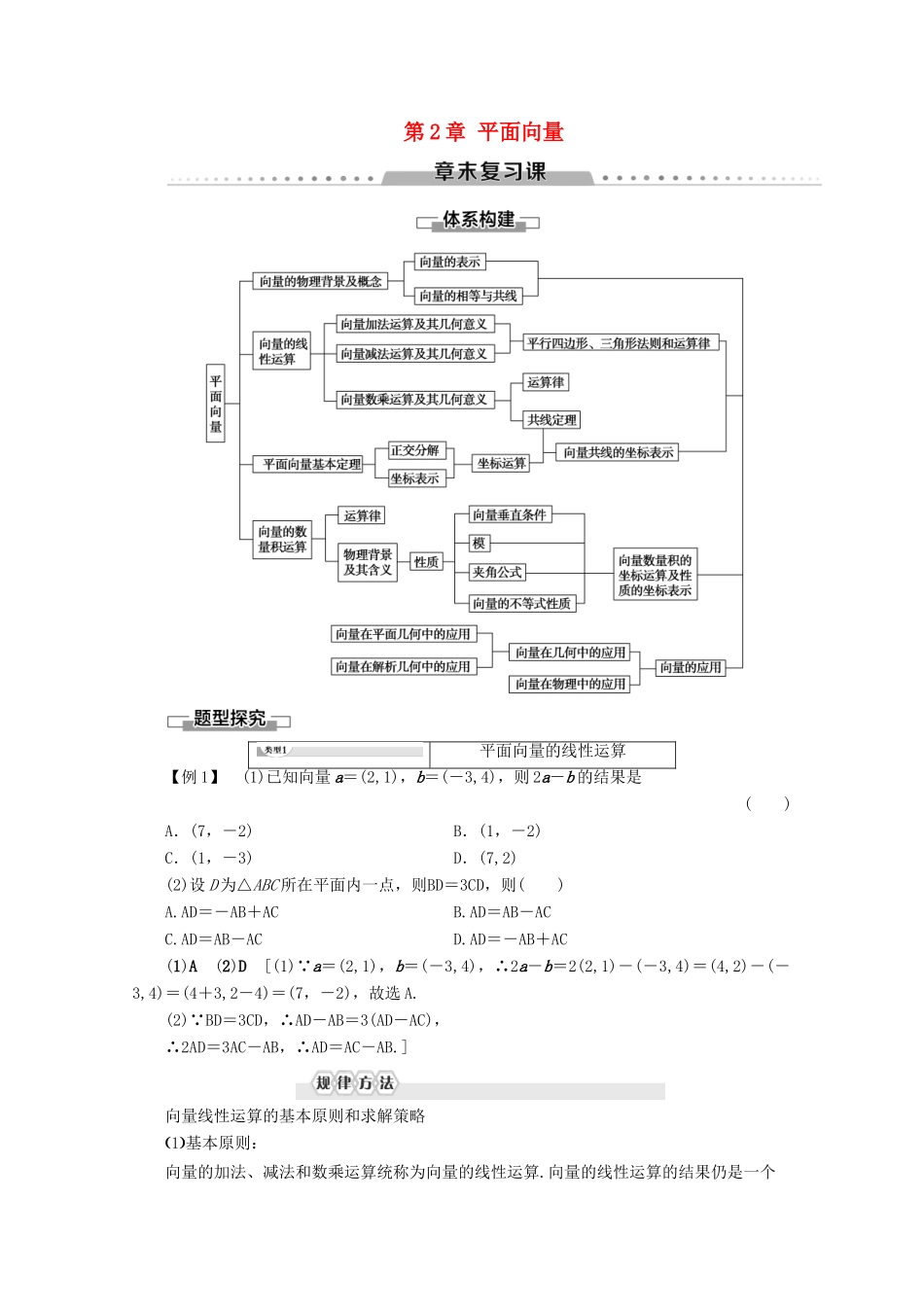
第 2 章 平面向量平面向量的线性运算【例 1】 (1)已知向量 a=(2,1),b=(-3,4),则 2a-b 的结果是( )A.(7,-2) B.(1,-2)C.(1,-3)D.(7,2)(2)设 D 为△ABC 所在平面内一点,则BD=3CD,则( )A.AD=-AB+ACB.AD=AB-ACC.AD=AB-ACD.AD=-AB+AC(1)A (2)D [(1) a=(2,1),b=(-3,4),∴2a-b=2(2,1)-(-3,4)=(4,2)-(-3,4)=(4+3,2-4)=(7,-2),故选 A.(2) BD=3CD,∴AD-AB=3(AD-AC),∴2AD=3AC-AB,∴AD=AC-AB.]向量线性运算的基本原则和求解策略1基本原则:向量的加法、减法和数乘运算统称为向量的线性运算.向量的线性运算的结果仍是一个向量,因此,对它们的运算法则、运算律的理解和运用要注意向量的大小和方向两个方面.2求解策略:① 向量是一个有“形”的几何量,因此在进行向量线性运算时,一定要结合图形,这是研究平面向量的重要方法与技巧.② 字符表示线性运算的常用技巧:,首尾相接用加法的三角形法则,如AB+BC=AC;共起点两个向量作差用减法的几何意义,如OB-OA=AB.③ 平行向量共线向量、相等向量与相反向量、单位向量等,理解向量的有关概念并进行恰当地应用.④ 注意常见结论的应用.如△ABC 中,点 D 是 BC 的中点,则AB+AC=AD.1.(1)设向量 a,b 不平行,向量 λa+b 与 a+2b 平行,则实数 λ=________.(2)在△ABC 中,点 M,N 满足AM=2MC,BN=NC.若MN=xAB+yAC,则 x=________;y=________.(1) (2) - [(1)因为 λa+b 与 a+2b 平行,所以 λa+b=t(a+2b),即 λa+b=ta+2tb,所以解得(2)因为AM=2MC,所以AM=AC.因为BN=NC,所以AN=(AB+AC),所以MN=AN-AM=(AB+AC)-AC=AB-AC.又MN=xAB+yAC,所以 x=,y=-.]平面向量的数量积【例 2】 (1)设单位向量 m=(x,y),b=(2,-1).若 m⊥b,则|x+2y|=________.(2)已知两个单位向量 a,b 的夹角 θ 为 60°,c=ta+(1-t)b,若 b·c=0,则 t=________.(1) (2)2 [(1)因为单位向量 m=(x,y),则 x2+y2=1.①若 m⊥b,则 m·b=0,即 2x-y=0.②由①②解得 x2=,所以|x|=,|x+2y|=5|x|=.(2)法一:因为 b·c=0,所以 b·[ta+(1-t)b]=0,即 ta·b+(1-t)b2=0.又因为|a|=|b|=1,θ=60°,所以 t+1-t=0,所以 t=2.法二:由 t+(1-t)=1 知向量 a,b,c 的终点 A、B、C 共线,在平面直角坐标系中设 a=(1,...