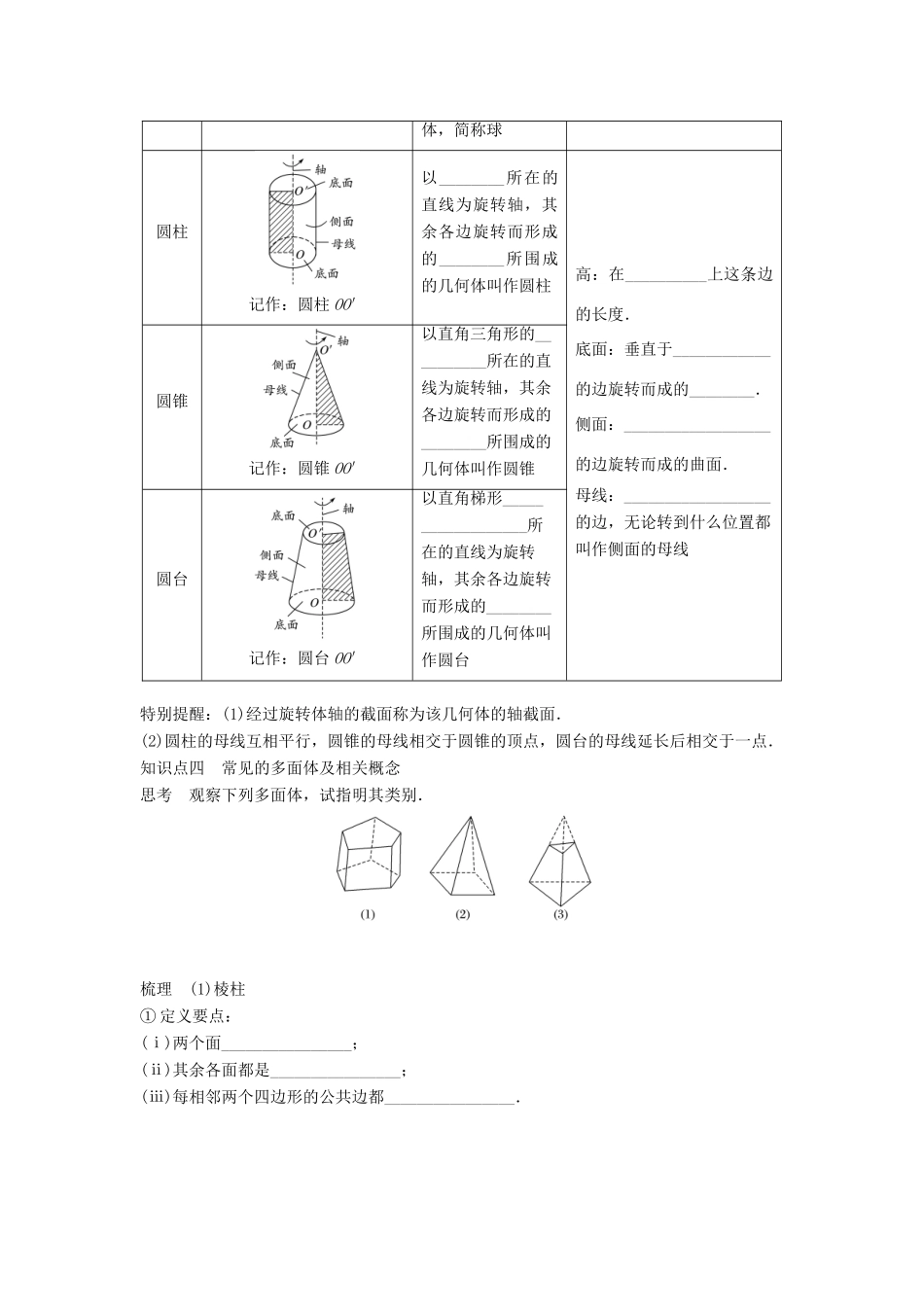
1 简单几何体学习目标 1.理解旋转体与多面体的概念.2.掌握球、圆柱、圆锥、圆台的结构特征.3.掌握棱柱、棱锥、棱台的基本性质.知识点一 两平面平行和直线与平面垂直的概念思考 1 如何定义两平面平行? 思考 2 如何判定直线与平面垂直? 梳理 (1)________________的两个平面平行.(2)如果一条直线与一个平面内的__________________都垂直,则这条直线与这个平面垂直.知识点二 旋转体与多面体旋转体一条__________绕着它所在的平面内的一条定直线旋转所形成的曲面叫作____________;封闭的旋转面围成的几何体叫作______________多面体把若干个________________围成的几何体叫作________________知识点三 常见的旋转体及概念思考 1 以直角三角形的一条直角边所在的直线为轴旋转 180°所得的旋转体是圆锥吗? 思考 2 能否由圆锥得到圆台? 梳理 名称图形及表示定义相关概念球记作:球 O球面:以________________ 所 在 的 直线为旋转轴,将半圆旋转所形成的________叫作球面.球体:球面所围成的 几 何 体 叫 作 球球心:半圆的________.球的半径:连接球心和球面上任意一点的线段.球的直径:连接__________上两点并且过______的线段体,简称球圆柱记作:圆柱 OO′以________所在的直线为旋转轴,其余各边旋转而形成的________所围成的几何体叫作圆柱高:在__________上这条边的长度.底面:垂直于____________的边旋转而成的________.侧面:__________________的边旋转而成的曲面.母线:__________________的边,无论转到什么位置都叫作侧面的母线圆锥记作:圆锥 OO′以直角三角形的__________所在的直线为旋转轴,其余各边旋转而形成的________所围成的几何体叫作圆锥圆台记作:圆台 OO′以直角梯形_____ _____________所在的直线为旋转轴,其余各边旋转而形成的________所围成的几何体叫作圆台特别提醒:(1)经过旋转体轴的截面称为该几何体的轴截面.(2)圆柱的母线互相平行,圆锥的母线相交于圆锥的顶点,圆台的母线延长后相交于一点.知识点四 常见的多面体及相关概念思考 观察下列多面体,试指明其类别. 梳理 (1)棱柱① 定义要点:(ⅰ)两个面________________;(ⅱ)其余各面都是________________;(ⅲ)每相邻两个四边形的公共边都________________.② 相关概念:底面:两个________________的面.侧面:除底面外的其余各面.侧棱:相邻______________的公共边.顶点:底面多边形与________的公...