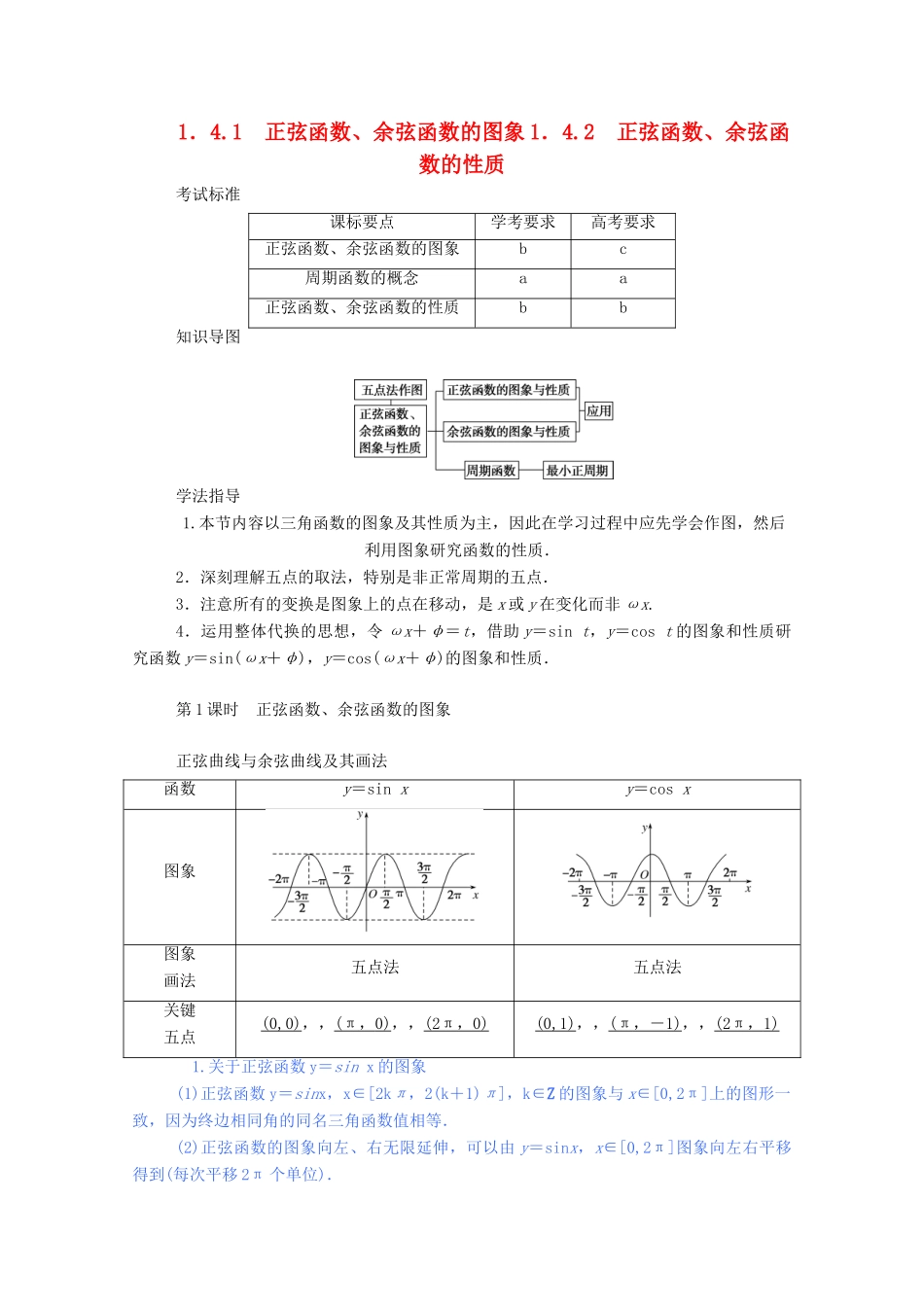
1.4.1 正弦函数、余弦函数的图象 1.4.2 正弦函数、余弦函数的性质考试标准课标要点学考要求高考要求正弦函数、余弦函数的图象bc周期函数的概念aa正弦函数、余弦函数的性质bb知识导图学法指导1.本节内容以三角函数的图象及其性质为主,因此在学习过程中应先学会作图,然后利用图象研究函数的性质.2.深刻理解五点的取法,特别是非正常周期的五点.3.注意所有的变换是图象上的点在移动,是 x 或 y 在变化而非 ωx.4.运用整体代换的思想,令 ωx+φ=t,借助 y=sin t,y=cos t 的图象和性质研究函数 y=sin(ωx+φ),y=cos(ωx+φ)的图象和性质.第 1 课时 正弦函数、余弦函数的图象正弦曲线与余弦曲线及其画法函数y=sin xy=cos x图象图象画法五点法五点法关键五点(0,0),,(π , 0) ,,(2π , 0) (0,1),,(π ,- 1) ,,(2π , 1) 1.关于正弦函数 y=sin x 的图象(1)正弦函数 y=sinx,x∈[2kπ,2(k+1)π],k∈Z 的图象与 x∈[0,2π]上的图形一致,因为终边相同角的同名三角函数值相等.(2)正弦函数的图象向左、右无限延伸,可以由 y=sinx,x∈[0,2π]图象向左右平移得到(每次平移 2π 个单位).2.“几何法”和“五点法”画正、余弦函数的比较(1)“几何法”就是利用单位圆中正弦线和余弦线作出正、余弦函数图象的方法 . 该方法作图较精确,但较为烦琐.(2)“五点法”是画三角函数图象的基本方法,在要求精度不高的情况下常用此法.提醒:作图象时,函数自变量要用弧度制,自变量与函数值均为实数,因此在 x 轴、y轴上可以统一单位,这样作出的图象正规便于应用.[小试身手]1.判断下列命题是否正确. (正确的打“√”,错误的打“×”)(1)“五点法”作正、余弦函数的图象时的“五点”是指图象上的任意五点.( )(2)正弦函数在和上的图象相同.( )(3)正弦函数、余弦函数的图象分别向左、右无限延伸.( )答案:(1)× (2)√ (3)√2.以下对正弦函数 y=sin x 的图象描述不正确的是( )A.在 x∈[2kπ,2(k+1)π](k∈Z)上的图象形状相同,只是位置不同B.介于直线 y=1 与直线 y=-1 之间C.关于 x 轴对称D.与 y 轴仅有一个交点解析:画出 y=sin x 的图象,根据图象可知 A,B,D 三项都正确.答案:C3.下列图象中,是 y=-sin x 在[0,2π]上的图象的是( )解析:函数 y=-sin x 的图象与函数 y=sin x 的图象关于 x 轴对称,故选 D.答案:...