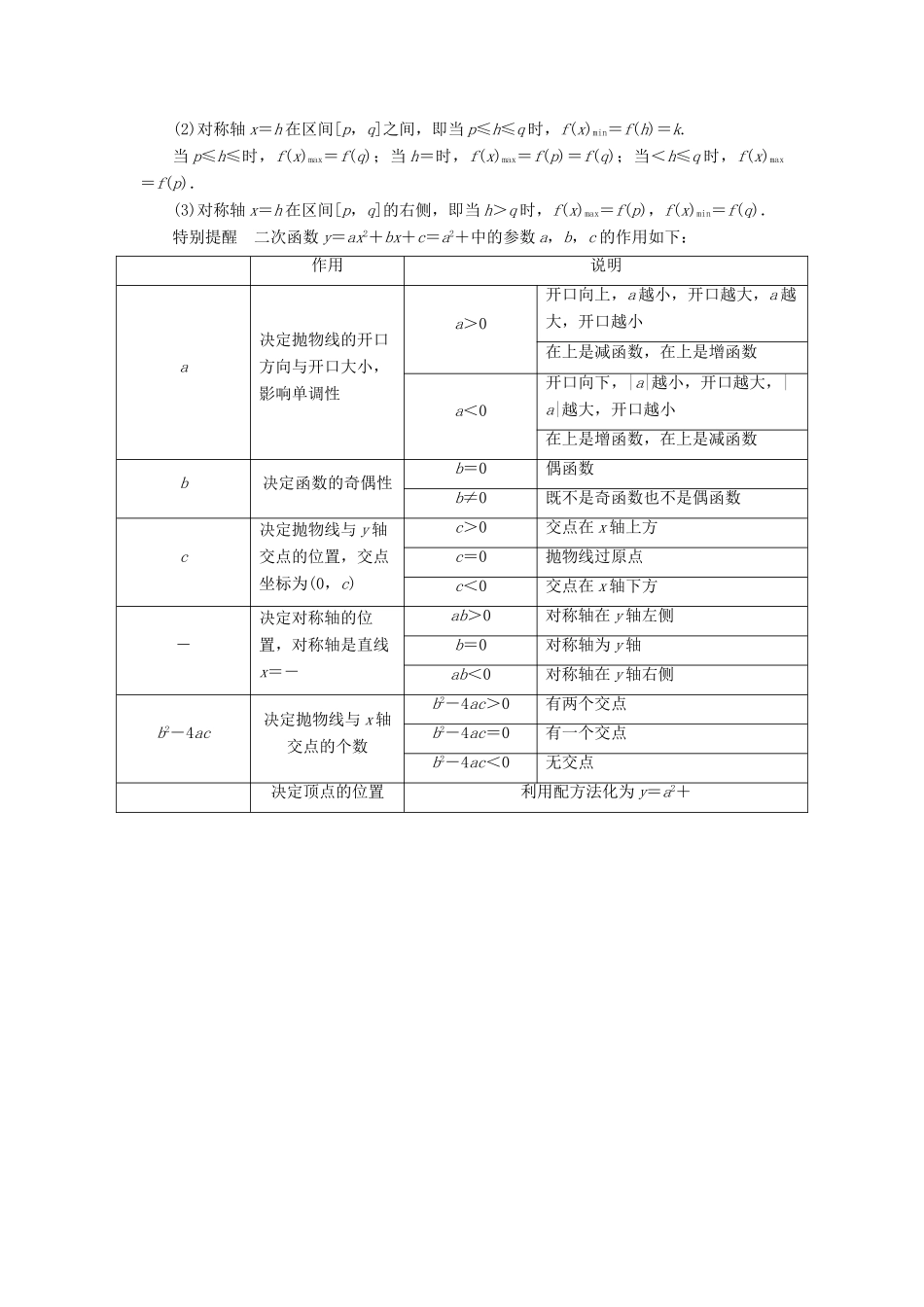
2.2.2 二次函数的性质与图象预习导航课程目标学习脉络1.掌握二次函数的性质与图象,学会用配方法研究二次函数的性质.2.掌握作二次函数图象的一般方法,学会运用函数图象理解和研究函数的性质.3.学会用从特殊到一般的思想方法来研究二次函数,并注意与初中所学知识的类比和联系.1.二次函数的定义函数 y = ax 2 + bx + c ( a ≠0) 叫做二次函数,它的定义域是 R.思考 1 函数 y=ax2+bx+c 为奇函数的条件是什么?提示:当 a=c=0,且 b≠0 时,y=ax2+bx+c=bx 是奇函数,故函数 y=ax2+bx+c为奇函数的条件是 a=c=0,b≠0.2.二次函数的性质与图象函数二次函数 y=ax2+bx+c(a,b,c 是常数,a≠0)图象a>0a<0性质① 抛物线开口向上,并向上无限延伸① 抛物线开口向下,并向下无限延伸② 对称轴是直线 x=-,顶点坐标是② 对称轴是直线 x=-,顶点坐标是③ 在区间上是减函数,在区间上是增函数③ 在区间上是增函数,在区间上是减函数④ 抛物线有最低点,当 x=-时,y有最小值,ymin=④ 抛物线有最高点,当 x=-时,y 有最大值,ymax=思考 2 二次函数 y=ax2+c 在 y 轴左侧是减函数,在右侧是增函数,对吗?提示:不对.当 a>0 时,函数在 y 轴左侧是减函数,在右侧是增函数;当 a<0 时,函数在 y 轴左侧是增函数,在右侧是减函数.思考 3 如何求二次函数在闭区间上的最值?提示:对于二次函数 y=ax2+bx+c(a>0)的最值问题,首先应采用配方法,化为 y=a(x-h)2+k(a>0)的形式.其解法是:抓住“三点一轴”数形结合,该讨论时要讨论.这里的“三点”指的是区间的两个端点和区间中点,“一轴”指的是对称轴.对于二次函数 f(x)=a(x-h)2+k(a>0)在区间[p,q]上的最值问题可作如下讨论:(1)对称轴 x=h 在区间[p,q]的左侧,即当 h<p 时,f(x)max=f(q),f(x)min=f(p).(2)对称轴 x=h 在区间[p,q]之间,即当 p≤h≤q 时,f(x)min=f(h)=k.当 p≤h≤时,f(x)max=f(q);当 h=时,f(x)max=f(p)=f(q);当<h≤q 时,f(x)max=f(p).(3)对称轴 x=h 在区间[p,q]的右侧,即当 h>q 时,f(x)max=f(p),f(x)min=f(q).特别提醒 二次函数 y=ax2+bx+c=a2+中的参数 a,b,c 的作用如下:作用说明a决定抛物线的开口方向与开口大小,影响单调性a>0开口向上,a 越小,开口越大,a 越大,开口越小在上是减函数,在上是增函数a<0...