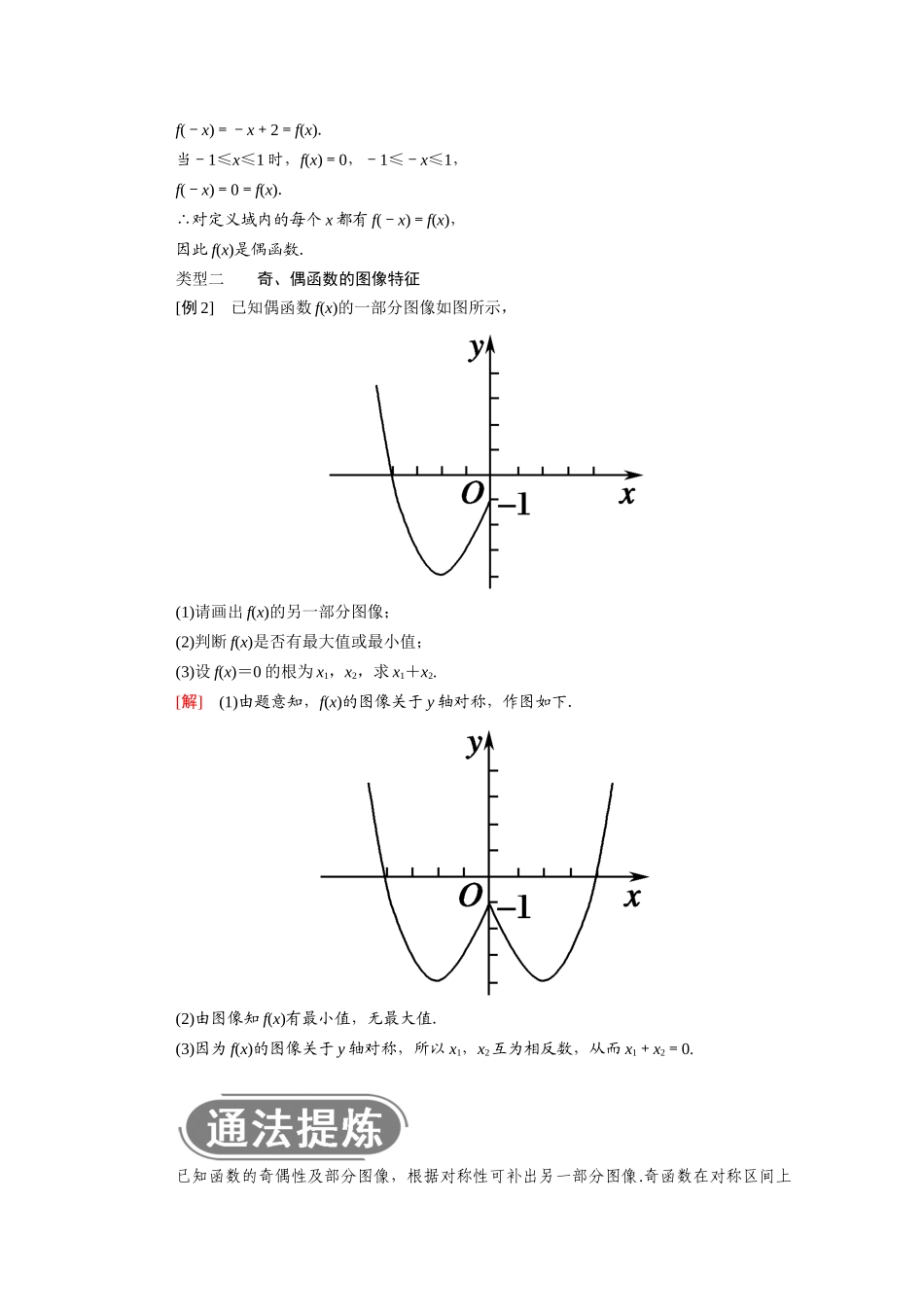
3.1.3 函数的奇偶性第 1 课时 函数的奇偶性(1)[课程目标] 1.结合具体函数,了解函数的奇偶性的含义;2.会根据奇偶性的定义判断和证明函数的奇偶性;3.会利用奇偶性来研究函数的定义域、值域、解析式、单调性及函数的图像等.知识点一 奇、偶函数的定义 [填一填](1)一般地,设函数 y=f(x)的定义域为 D,如果对 D 内的任意一个 x,都有-x∈D,且f(-x)=- f ( x ) ,则称 y=f(x)为奇函数.(2)一般地,设函数 y=f(x)的定义域为 D,如果对 D 内的任意一个 x,都有-x∈D,且f(-x)=f ( x ) ,则称 y=f(x)为偶函数.[答一答]1.从奇(偶)函数的定义来考虑,若对于奇(偶)函数定义域内的任意一个自变量 x,它的相反数-x 也在定义域内吗?由此得到什么结论?y=x2,x∈[-1,1)是偶函数吗?提示:在函数的定义域内,奇(偶)函数的定义域是对称的.y=x2,x∈[-1,1)不是偶函数,原因是 f(-1)≠f(1).(f(1)不存在)2.若奇函数 f(x)在 x=0 处有意义,则 f(0)等于什么?提示: f(-x)=-f(x),∴f(0)=-f(0),即 2f(0)=0,f(0)=0.知识点二 奇、偶函数的图像特征 [填一填]1.如果一个函数是奇函数,则这个函数的图像是以原点为对称中心的中心对称图形;反之,如果一个函数的图像是以原点为对称中心的中心对称图形,则这个函数是奇函数.2.如果一个函数是偶函数,则它的图像是以 y 轴 为对称轴的轴对称图形;反之,如果一个函数的图像关于 y 轴 对称,则这个函数是偶函数.[答一答]3.观察下列函数的图像,判断函数的奇偶性.提示:由题图可看出①②的图像均关于 y 轴对称,所以这两个函数均为偶函数;③④ 的图像关于原点对称,所以这两个函数均为奇函数.类型一 判断函数的奇偶性 [例 1] 判断下列函数的奇偶性:(1)f(x)=x2-2x;(2)f(x)=x3+;(3)f(x)=+;(4)f(x)=2-|x|.[解] (1)f(x)的定义域为 R,关于原点对称.因为 f(-x)=(-x)2-2(-x)=x2+2x≠f(x),且 f(-x)≠-f(x),所以 f(x)为非奇非偶函数.(2)f(x)的定义域为(-∞,0)∪(0,+∞),关于原点对称.因为 f(-x)=(-x)3+=-(x3+)=-f(x),所以 f(x)为奇函数.(3)f(x)的定义域为{-1,1},是两个具体数,关于原点对称.又 f(-1)=f(1)=0,f(-1)=-f(1)=0,∴f(x)=+既是奇函数,又是偶函数.(4)f(x)的定义域为 R,关于原点对称.因为 f(-x)=2-|-x|=2-|x|=f(x),所以 f(x)是偶函数.[变式训...