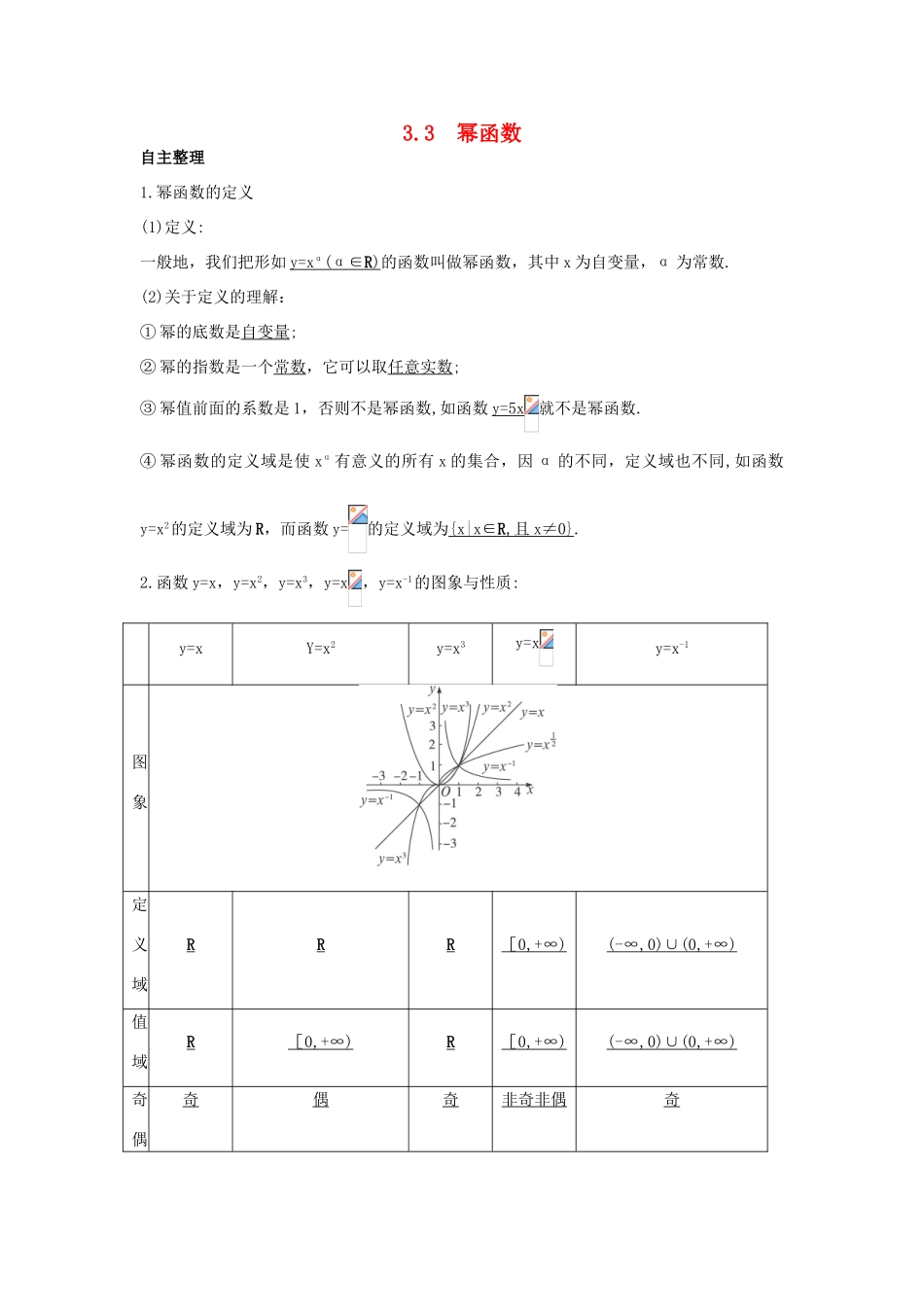
3.3 幂函数自主整理1.幂函数的定义(1)定义:一般地,我们把形如 y=x α (α∈ R ) 的函数叫做幂函数,其中 x 为自变量,α 为常数.(2)关于定义的理解:① 幂的底数是自变量;② 幂的指数是一个常数,它可以取任意实数;③ 幂值前面的系数是 1,否则不是幂函数,如函数 y=5x就不是幂函数.④ 幂函数的定义域是使 xα有意义的所有 x 的集合,因 α 的不同,定义域也不同,如函数y=x2的定义域为 R,而函数 y=的定义域为{x|x∈ R , 且 x≠0} .2.函数 y=x,y=x2,y=x3,y=x,y=x-1的图象与性质:y=xY=x2y=x3y=xy=x-1图象定义域RRR[ 0,+∞) (-∞,0)∪(0,+∞)值域R[ 0,+∞) R[ 0,+∞) (-∞,0)∪(0,+∞)奇偶奇偶奇非奇非偶奇性单调性增增增定点(0,0),(1,1)(0,0),(1,1)(0,0),(1,1)(0,0),(1,1)(1,1)3.幂函数的性质当 n>0 时,幂函数 y=xn有下列性质:(1)图象都通过点( 0 , 0 ),( 1 , 1 ) ;(2)在第一象限内,函数值 y 随 x 的增大而增大.当 n<0 时,幂函数 y=xn的性质:(1)图象都过点( 1 , 1 ) ;(2)图象以直线 x=0,y=0 为渐近线;(3)在第一象限内的图象是下降的,即函数值 y 随 x 的增大而减小;(4)x∈(0,1)时,n 越大曲线越靠近 y 轴;x∈(1,+∞)时,n 越小曲线越靠近 x 轴.高手笔记1.判断函数是否为幂函数时要根据定义,即 xα的系数为1,指数位置的 α 为一个常数,且常数项要为0,或者经过变形后满足条件的均可.2.在研究幂的性质时,通常将分数指数幂化为根式形式,负指数整数幂化为分式形式再去进行讨论.3.记忆口诀:如何分析幂函数,记住图象是关键,虽然指数各不同,分类之后变简单.大于 0 时抛物线,小于 0 时双曲线,还有 0 到 1 之间,抛物开口方向变,不仅开口向右方,原来图象取一半.函数奇偶看指数,奇母奇子奇函数,奇母偶子偶函数,偶母非奇偶函数.图象第一象限内,函数增减看正负.名师解惑1.如何理解幂函数的图象和性质?剖析:幂函数 y=xn的性质和图象,由于 n 的取值不同而比较复杂,我们可以从下面几个方面来把握:(1)n<0 时,图象不过原点,在第一象限内图象是下降的曲线,幂函数的图象在区间(0,+∞)上是减函数.在第一象限内,当 x 从右边趋向原点时,图象在 y 轴右方无限地逼近 y 轴正半轴,当 x 趋于+∞时,图象在 x 轴上方无限地逼近 x 轴正半轴.n>0 时,图象必经过原点和(1,1)两定点,在第一象限内图象是上...