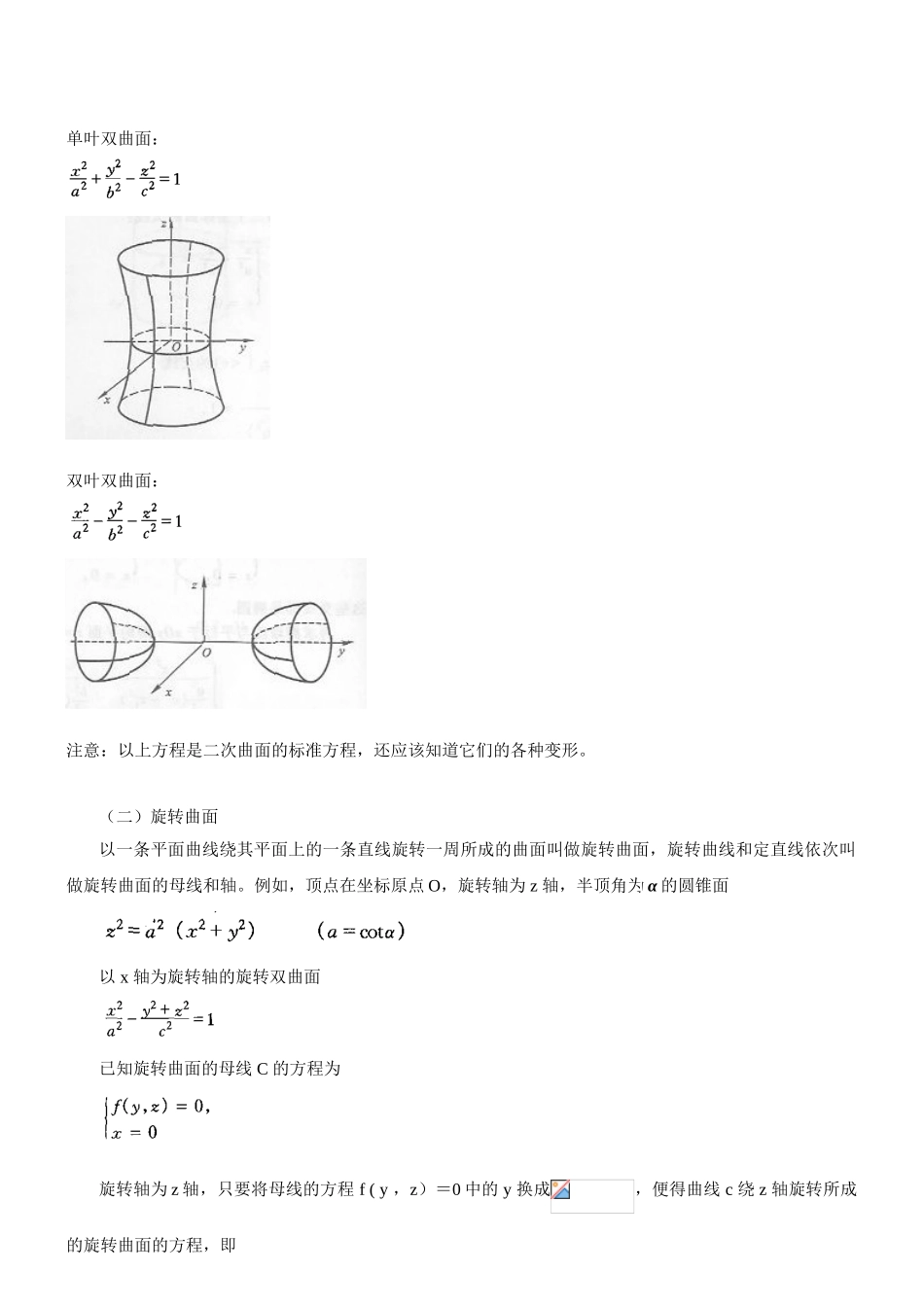
四、二次曲面 旋转曲面 柱面(一)二次曲面三元二次方程所表示的曲面叫做二次曲面。例如球面:椭球面:椭圆抛物面:双曲抛物面:单叶双曲面:双叶双曲面:注意:以上方程是二次曲面的标准方程,还应该知道它们的各种变形。(二)旋转曲面以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面叫做旋转曲面,旋转曲线和定直线依次叫做旋转曲面的母线和轴。例如,顶点在坐标原点 O,旋转轴为 z 轴,半顶角为 α 的圆锥面以 x 轴为旋转轴的旋转双曲面已知旋转曲面的母线 C 的方程为旋转轴为 z 轴,只要将母线的方程 f ( y ,z)=0 中的 y 换成,便得曲线 c 绕 z 轴旋转所成的旋转曲面的方程,即同理,可得其他情形的旋转曲面的方程。(三)柱面平行于定直线并沿定曲线 C 移动的直线 L 形成的轨迹叫做柱面,定曲线 C 叫做柱面的准线,动直线 L 叫做柱面的母线。例如,以 xOy 平面上的圆 x2+y2= R2 为准线,平行于 z 轴的直线为母线的圆柱面以 xOy 平面上的抛物线 y2=2x 为准线,平行于 z 轴的直线为母线的抛物柱面在空间直角坐标系中,假如曲面方程 F ( x , y ,z)= 0 中,缺少某个变量,那么该方程一般表示一个柱面。例如,方程 F ( x ,y)=0 一般表示一个母线平行于 z 轴的柱面,方程 G ( x , z )=0 , H ( y , z ) =0 一般表示一个母线平行于 y 轴,x 轴的柱面。(四)例题 【 例 1-1-11 】方程 z2-x2-y2=0 所表示的曲面是 ( A )单叶双曲面 ( B )双叶双曲面 ( C )旋转双曲面 ( D )圆锥面 【 解 】 在顶点位于原点、旋转轴为 z 轴的圆锥面方程中,令 a = 1 ,即为所给方程,故选( D )。【例 1-1-12 】将双曲线 C绕 x 轴旋转一周所生成的旋转曲面的方程是【 解 】 曲线 C 绕 x 轴旋转,只需将 C 的方程中的 y 换成,故应选( B )。 五、空间曲线空间曲线可以看作是两下曲面的交线。若空间曲线 C 是曲面的交线,则 C 的方程可用下述方程组表示此方程组称为空间曲线 C 的一般方程。若将空间曲线 C 上动点的坐标 x 、y、 z 表示为参数 t 的函数:这方程组称为空间曲线 C 的参数方程。例如,参数方程表示的空间曲线是螺旋线。第二节微分学一、极限(一)函数的几种特性(二)函数的极限 1 . 函数极限的概念 无穷小与无穷大 函数的极限按自变量的变化趋向、。可分成以下两种。当时...