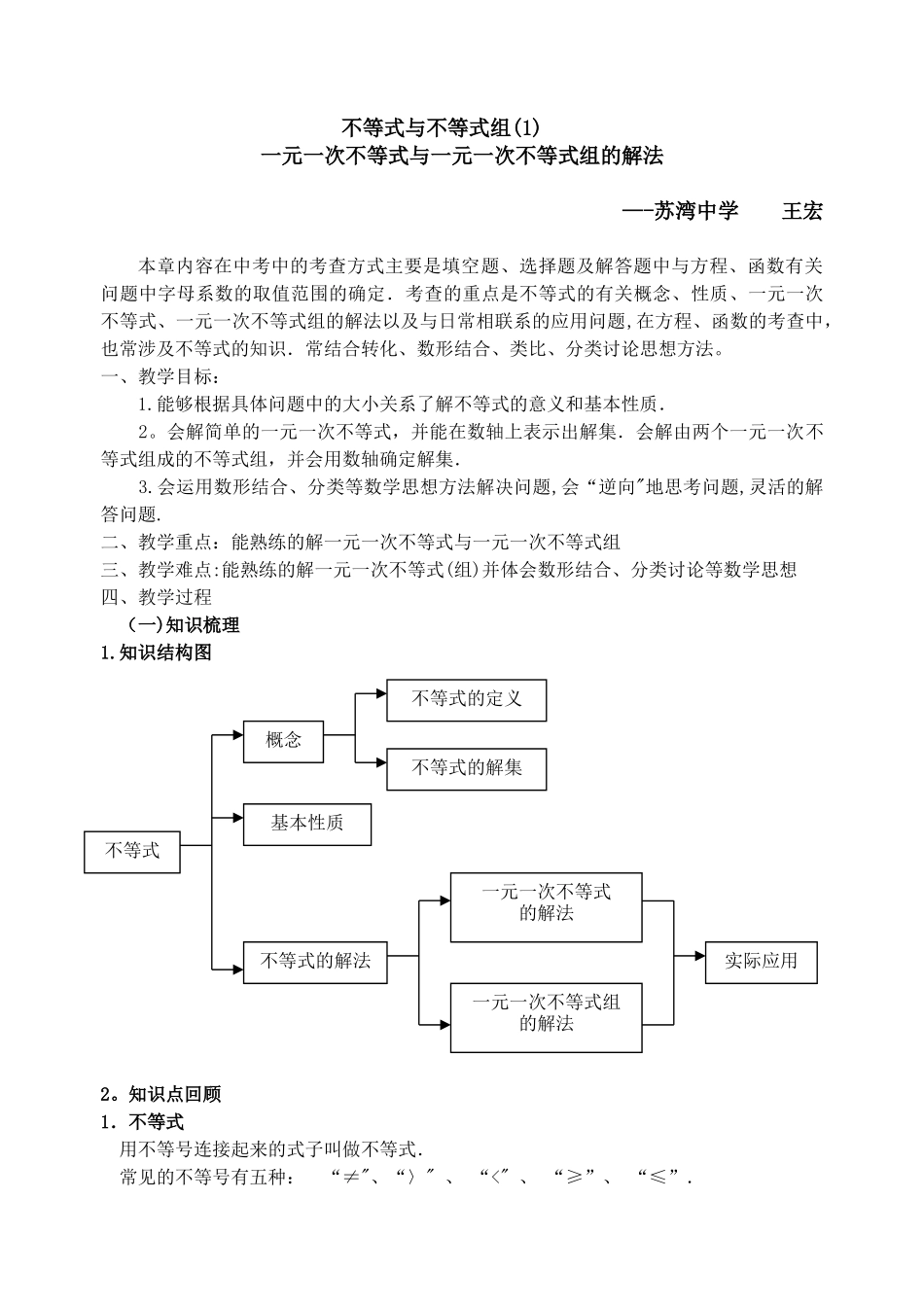
不等式与不等式组(1) 一元一次不等式与一元一次不等式组的解法—-苏湾中学 王宏本章内容在中考中的考查方式主要是填空题、选择题及解答题中与方程、函数有关问题中字母系数的取值范围的确定.考查的重点是不等式的有关概念、性质、一元一次不等式、一元一次不等式组的解法以及与日常相联系的应用问题,在方程、函数的考查中,也常涉及不等式的知识.常结合转化、数形结合、类比、分类讨论思想方法。一、教学目标: 1.能够根据具体问题中的大小关系了解不等式的意义和基本性质. 2。会解简单的一元一次不等式,并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集. 3.会运用数形结合、分类等数学思想方法解决问题,会“逆向"地思考问题,灵活的解答问题.二、教学重点:能熟练的解一元一次不等式与一元一次不等式组三、教学难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想四、教学过程(一)知识梳理1.知识结构图2。知识点回顾1.不等式 用不等号连接起来的式子叫做不等式. 常见的不等号有五种: “≠"、“〉" 、 “<" 、 “≥”、 “≤”.概念基本性质不等式的定义不等式的解法一元一次不等式的解法一元一次不等式组的解法不等式实际应用不等式的解集2.不等式的解与解集 不等式的解:使不等式成立的未知数的值,叫做不等式的解.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点.解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左. 说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值.3.不等式的基本性质 (1)不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.假如,那么 (2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.假如,那么(或)(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.假如那么(或)说明:任意两个实数 a、b 的大小关系:① a—b>Oa>b;② a-b=Oa=b;③ a—bO 或 ax+b〈O(a≠O,a,b 为已知数). 5.解一元一次不等式的一般步骤 解一元一...