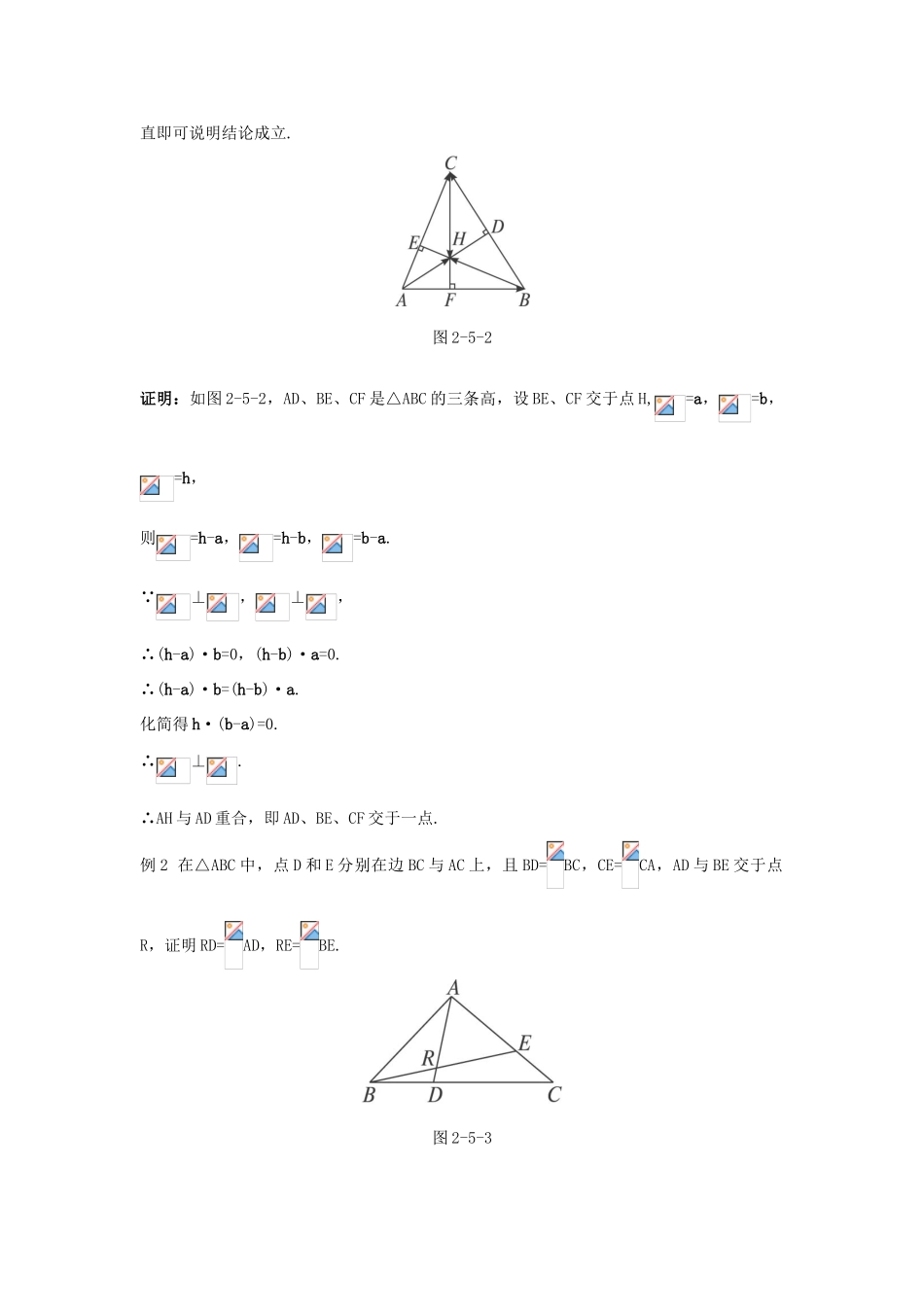
2.5.1 平面几何中的向量方法 2.5.2 向量在物理中的应用举例疱工巧解牛知识•巧学一、平面几何中的向量方法 用向量知识证明平面几何问题是向量应用的一个方面,解决这类题的关键是正确选择基底,表示出相关向量,这样平面图形的许多性质,如长度、夹角等都可以通过向量的线性运算及数量积表示出来,从而把几何问题转化成向量问题,再通过向量的运算法则运算就可以达到解决几何问题的目的了. 用向量法(即以向量和向量的运算为工具,对几何元素及其关系进行讨论)证明几何问题需把点、线、面等几何要素直接归为向量,对这些向量借助于它们之间的运算进行讨论然后把这些结果翻译成点、线、面的相应结果,可简单地表述为:〔形到向量〕——〔向量的运算〕——〔向量和数到形〕.学法一得 用向量法证明几何问题的“三步曲”:①建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;②通过向量运算研究几何元素之间的关系,如距离、夹角等问题;③把运算结果“翻译”成几何关系.二、向量在物理中的应用 向量还具有强烈的物理学实际背景.物理学中有两种基本量:标量和矢量.矢量遍布在物理学的很多分支,它包括力、位移、速度、加速度、动量等.虽然,物理学中的矢量与数学中的向量并不完全相同,例如力,它除了有方向和大小,还有作用点;数学中的向量则只有方向和大小,没有作用点.但是,这并不影响向量在物理学中的作用.学法一得 向量在物理中的应用,实际上就是先把物理问题转化成数学问题,然后通过向量运算解决向量问题,最后再用所获得的结果解释物理现象.在学习过程中,一要体会如何把物理问题转化成数学问题,即如何将物理量之间的关系抽象成数学模型,二要体会如何利用数学模型的解来解释物理现象.典题•热题知识点一 用向量方法证明几何问题例 1 已知 AD、BE、CF 分别是△ABC 的三条高,求证:AD、BE、CF 相交于同一点.思路分析:本题主要考查向量在几何中的应用.通常情况下,用向量作工具证明几何问题时,往往要先设一些向量作为基本向量,我们假设两条高 BE、CF 交于点 H,再证明 AD 与 BC 垂直即可说明结论成立.图 2-5-2证明:如图 2-5-2,AD、BE、CF 是△ABC 的三条高,设 BE、CF 交于点 H,=a,=b,=h,则=h-a,=h-b,=b-a. ⊥,⊥,∴(h-a)·b=0,(h-b)·a=0.∴(h-a)·b=(h-b)·a.化简得 h·(b-a)=0.∴⊥.∴AH 与 AD 重合,即 AD、BE、CF 交于一点.例 2 在△ABC...