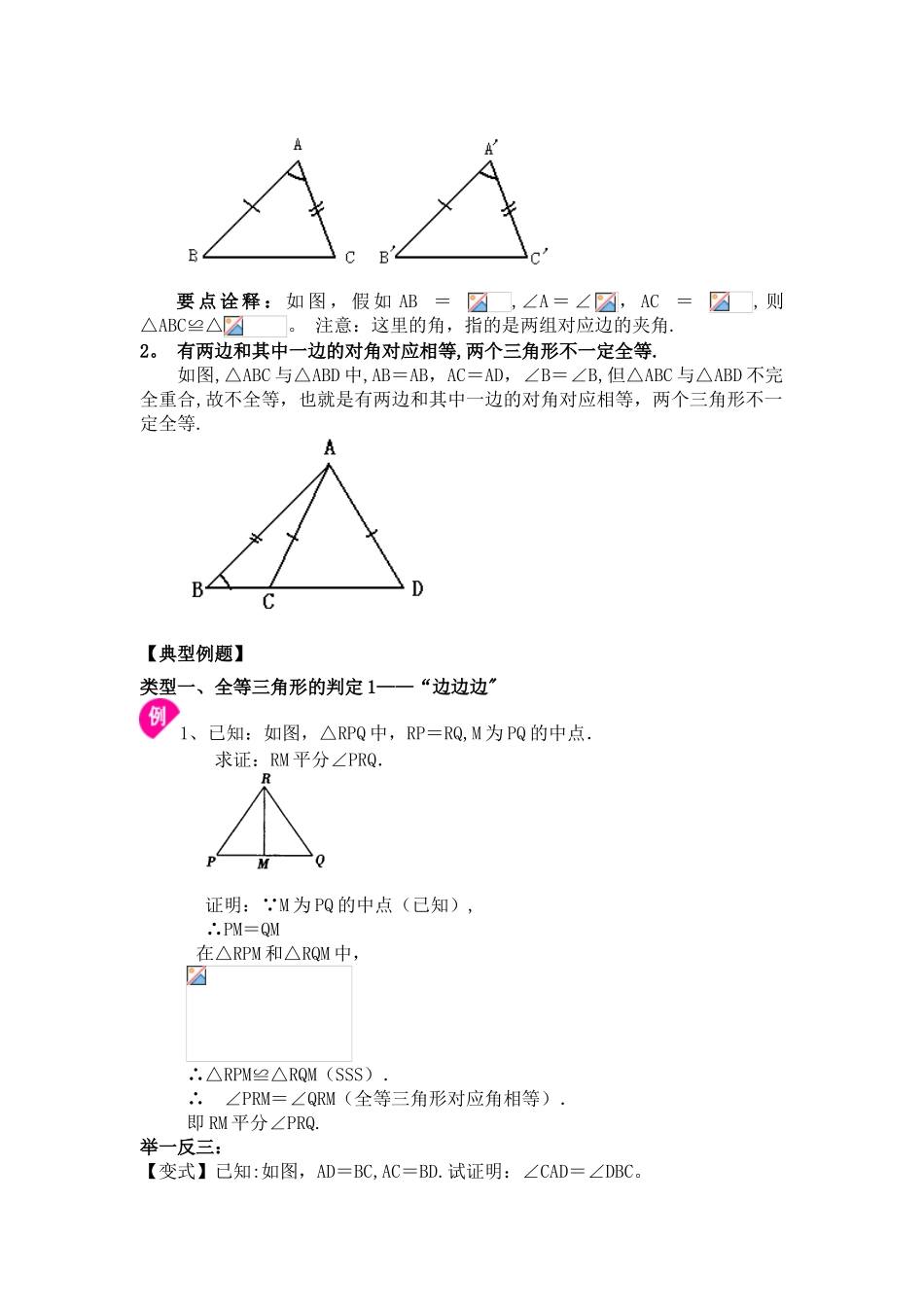
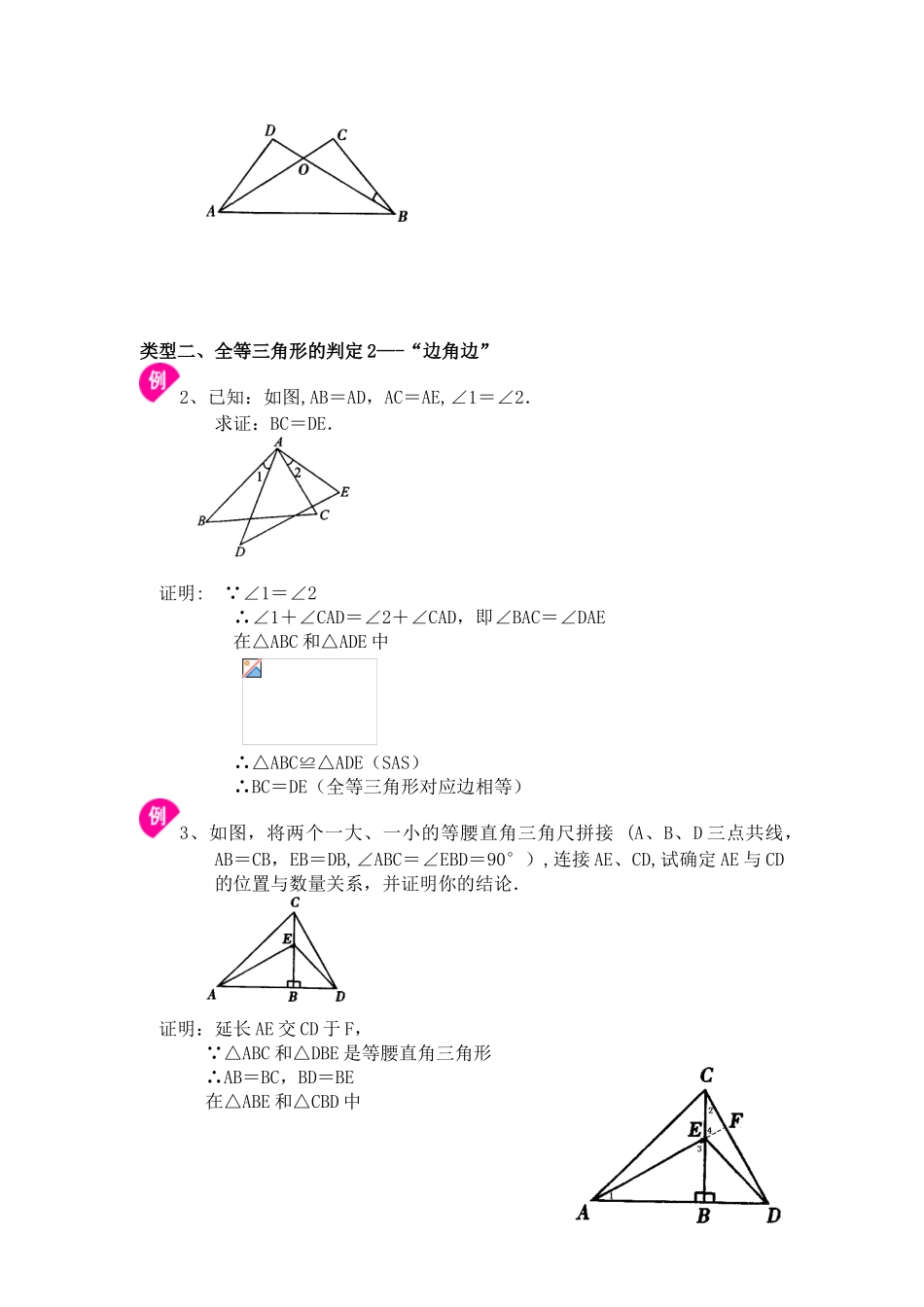
全等三角形的性质和判定要点一、全等三角形的概念能够完全重合的两个三角形叫全等三角形。要点二、对应顶点,对应边,对应角1。 对应顶点,对应边,对应角定义两个全等三角形重合在一起,重合的顶点叫对应顶点,重合的边叫对应边,重合的角叫对应角.要点诠释:在写两个三角形全等时,通常把对应顶点的字母写在对应位置上,这样容易找出对应边、对应角。如下图,△ABC 与△DEF 全等,记作△ABC≌△DEF,其中点 A 和点 D,点 B 和点 E,点 C 和点 F 是对应顶点;AB 和 DE,BC 和 EF,AC 和 DF 是对应边;∠A 和∠D,∠B 和∠E,∠C 和∠F 是对应角.要点三、全等三角形的性质 全等三角形的对应边相等;全等三角形的对应角相等。要点四、全等三角形的判定 (SSS、SAS、ASA、AAS、HL)全等三角形判定一(SSS,SAS)全等三角形判定 1-—“边边边”三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS”).要点诠释 :如图,假如=AB,=AC,=BC,则△ABC≌△。 要点二、全等三角形判定 2——“边角边”1。 全等三角形判定 2——“边角边”两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边 "或“SAS”)。要 点 诠 释 : 如 图 , 假 如 AB = ,∠A = ∠, AC = , 则△ABC≌△。 注意:这里的角,指的是两组对应边的夹角.2。 有两边和其中一边的对角对应相等,两个三角形不一定全等.如图,△ABC 与△ABD 中,AB=AB,AC=AD,∠B=∠B,但△ABC 与△ABD 不完全重合,故不全等,也就是有两边和其中一边的对角对应相等,两个三角形不一定全等.【典型例题】类型一、全等三角形的判定 1——“边边边"1、已知:如图,△RPQ 中,RP=RQ,M 为 PQ 的中点.求证:RM 平分∠PRQ.证明: M 为 PQ 的中点(已知),∴PM=QM在△RPM 和△RQM 中,∴△RPM≌△RQM(SSS).∴ ∠PRM=∠QRM(全等三角形对应角相等).即 RM 平分∠PRQ.举一反三:【变式】已知:如图,AD=BC,AC=BD.试证明:∠CAD=∠DBC。类型二、全等三角形的判定 2—-“边角边”2、已知:如图,AB=AD,AC=AE,∠1=∠2.求证:BC=DE.证明: ∠1=∠2 ∴∠1+∠CAD=∠2+∠CAD,即∠BAC=∠DAE 在△ABC 和△ADE 中 ∴△ABC≌△ADE(SAS) ∴BC=DE(全等三角形对应边相等)3、如图,将两个一大、一小的等腰直角三角尺拼接 (A、B、D 三点共线,AB=CB,EB=DB,∠ABC=∠EBD=90°),连接 AE、CD,试确定...