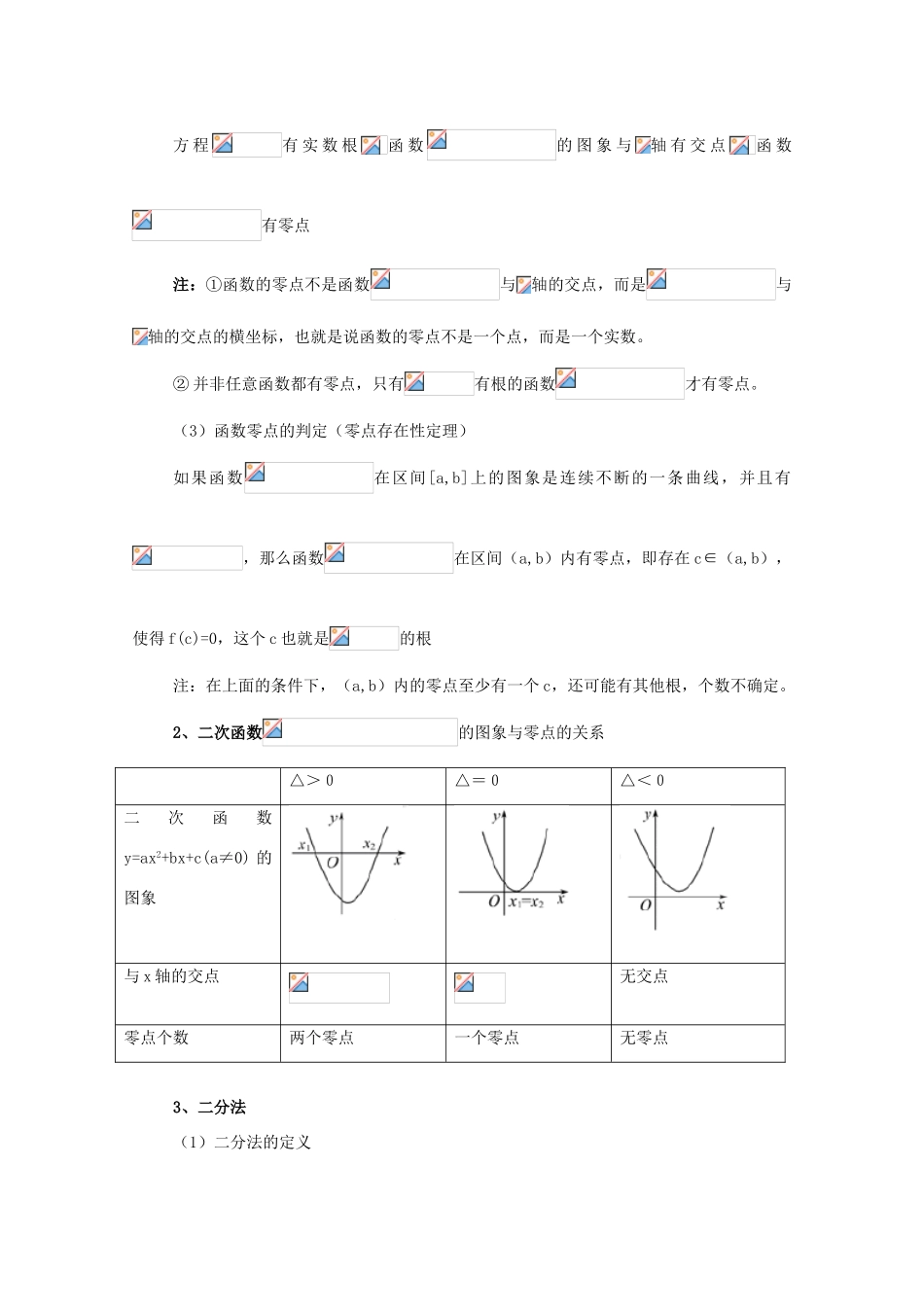
2011 年高三数学一轮精品复习学案:函数、导数及其应用第六节 函数应用【高考目标定位】一、函数与方程1、考纲点击(1)结合二次函数的图象,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数。(2)根据具体函数的图象,能够用二分法求相应方程的近似解。2、热点提示(1)函数与方程的零点、二分法是新课标的新增内容,在近年的高考中一定有所体现。(2)本节内容多以选择题、填空题的形式出现,属中低档题,不排除与其他知识,在知识交汇处命题。二、函数模型及其应用1、考纲点击(1)了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义。(2)了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用。2、热点提示(1)考查数学建模能力以及分析问题、解决问题的能力;几种增长型函数模型的应用可能会成为明年高考的又一生长点。(2)多以解答题的形式出现,属中、高档题,偶尔也会在选择题、填空题中考查。【考纲知识梳理】一、函数与方程1、函数的零点(1)函数零点的定义对于函数,把使成立的实数叫做函数的零点。(2)几个等价关系方 程有 实 数 根函 数的 图 象 与轴 有 交 点函 数有零点注:①函数的零点不是函数与轴的交点,而是与轴的交点的横坐标,也就是说函数的零点不是一个点,而是一个实数。② 并非任意函数都有零点,只有有根的函数才有零点。(3)函数零点的判定(零点存在性定理)如果函数在区间[a,b]上的图象是连续不断的一条曲线,并且有,那么函数在区间(a,b)内有零点,即存在 c∈(a,b),使得 f(c)=0,这个 c 也就是的根注:在上面的条件下,(a,b)内的零点至少有一个 c,还可能有其他根,个数不确定。2、二次函数的图象与零点的关系△>0△=0△<0二次函数y=ax2+bx+c(a≠0) 的图象与 x 轴的交点无交点零点个数两个零点一个零点无零点 3、二分法(1)二分法的定义对于在区间[a,b]上连续不断且的函数,通过不断地把函数的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。(2)用二分法求函数零点近似值的步骤第一步,确定区间[a,b],验证,给定精确度;第二步,求区间(a,b)的中点;第三步,计算:① 若=0,则就是函数的零点;② 若,则令(此时零点);③ 若,则令(此时零点);第四步,判断是否达到精确度:即若...