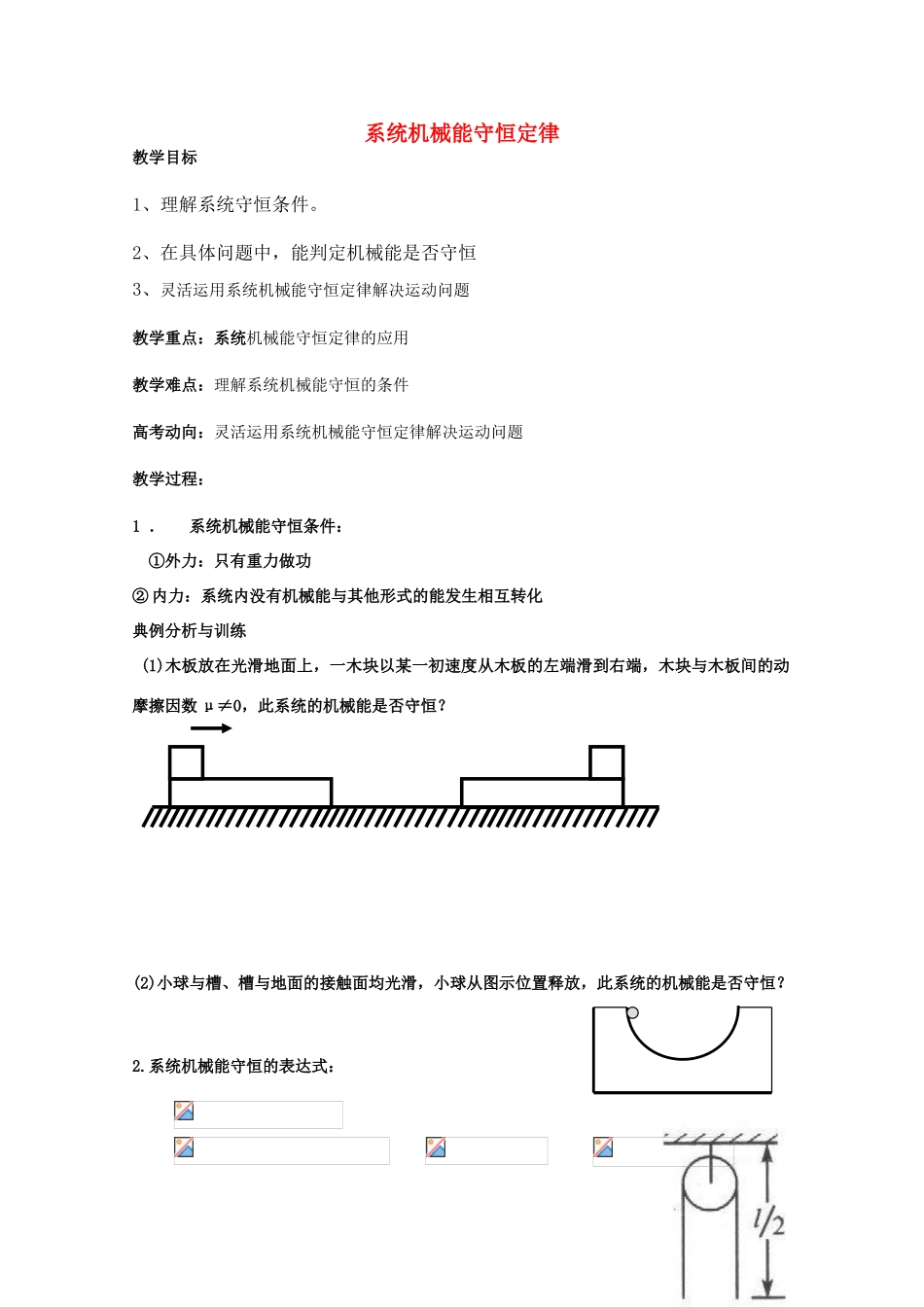
系统机械能守恒定律教学目标1、理解系统守恒条件。2、在具体问题中,能判定机械能是否守恒3、灵活运用系统机械能守恒定律解决运动问题教学重点:系统机械能守恒定律的应用教学难点:理解系统机械能守恒的条件高考动向:灵活运用系统机械能守恒定律解决运动问题教学过程:1 . 系统机械能守恒条件: ①外力:只有重力做功② 内力:系统内没有机械能与其他形式的能发生相互转化典例分析与训练 (1)木板放在光滑地面上,一木块以某一初速度从木板的左端滑到右端,木块与木板间的动摩擦因数 μ≠0,此系统的机械能是否守恒?(2)小球与槽、槽与地面的接触面均光滑,小球从图示位置释放,此系统的机械能是否守恒? 2.系统机械能守恒的表达式: 典例分析与训练例 1 如图所示,总长为 L 的光滑匀质铁链跨过一个光滑的轻小滑轮,开始时下端 A、B 相平齐,当略有扰动时其一端下落,则当铁链刚脱离滑轮的瞬间,铁链的速度为多大? 解析 这里提供两种解法。解法一(利用 E2=E1求解):设铁链单位长度的质量为 ρ,且选取初始位置铁链的下端A、B 所在的水平面为参考平面,则铁链初态的机械能为 ,末态的机械能为 。根据机械能守恒定律有 E2=E1,即 ,解得铁链刚脱离滑轮时的速度 。解法二(利用△Ek=-△Ep求解):如图所示,铁链刚离开滑轮时,相当于原来的 BB’部分移到了 AA’的位置。重力势能的减少量 ,动能的增加量 。根据机械能守恒定律有 △Ek=-△Ep,即 ,解得铁链刚脱离滑轮时的速度 。 点拨 对于绳索、链条之类的物体,由于发生形变,其重心位置相对物体来说并不是固定不变的,能否确定重心的位置,常是解决该类问题的关键。可以采用分段法求出每段的重力势能,然后求和即为整体的重力势能;也可采用等效法求出重力势能的改变量。再有,利ABL/2L/2B’A’用△Ek=-△Ep列方程时,不需要选取参考平面,且便于分析计算。对应练习:1.质量为 m 的长为 L 的均匀链条,放在离地高度为3L 的桌面上,链条的三分之一垂在桌面外,桌面光滑,链条无初速下 滑,当链条刚脱离桌面时速度为_________________,当链条下端刚触地时,链条的速度为_________________。答案:例 2 如图所示,半径为的光滑半圆上有两个小球,质量分别为,M>m,由细线挂着,今由静止开始自由释放,求小球升至最高点时两球的速度?对应练习: 如图所示,半径为的光滑半圆上有两个小球,质量分别为,由细线挂着,今由静止开始自由释放,当小球升至...