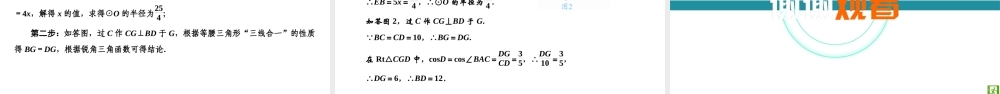专题综合强化第二部分 专题四 特殊图形的计算与证明• 【专题分析】特殊图形的计算与证明占据中考几何的大部分内容,每年均会出 2 道或 3 道题.主要考查类型:①特殊三角形的计算与证明[2016 . 13 ( 2 ) ] ;②特殊四边形的计算与证明 [2018 . 10 ; 2017 .6 ; 2017 . 13 ( 2 ); 2016 . 10 ; 2015 . 20 ; 2015 . 5] ;③与切线有关的计算与证明( 2018 . 20 ; 2017 . 21 ; 2016 . 18 ;2014 . 22 ).• 【类型特征】特殊三角形即为等腰、等边、直角三角形;而直角三角形还包括含30° , 45° 角的直角三角形.这些特殊三角形是中考中的高频考点,因为它能构成曲径通幽、灵活的优秀试题,有极为广泛的学习空间和命题空间.• 【解题策略】特殊三角形的解法主要是善于发现、充分挖掘、灵活运用特殊三角形的特有性质和一般性质;如当题中出现等腰三角形时,首先想到“三线合一”;若发现有直角三角形,立刻想到“勾股定理”,若是出现含 30° , 45° 角的直角三角形就要充分运用相关的特殊性质,解答时还特别注意等腰三角形存在着多解,它常与锐角三角函数、相似三角形、特殊四边形等知识相互利用来解决问题.常考题型 · 精讲类型一 特殊三角形的计算与证明例1 (2018·甘孜)如图,△ABC 中,AB=AC,∠BAC=90°,点 D,E 分别在 AB,BC 上,∠EAD=∠EDA,点 F 为 DE 的延长线与 AC 的延长线的交点.(1)求证:DE=EF; • 只要证明 EA = ED , EA = EF 即可解决问题.解题思路 【解答】证明: ∠BAC=90°, ∴∠EAD+∠CAE=90°,∠EDA+∠F=90°. ∠EAD=∠EDA,∴∠EAC=∠F,EA=ED, ∴EA=EF,∴DE=EF. • ( 2 )判断 BD 和 CF 的数量关系,并说明理由;解题思路 第一步:先给出结论:BD=CF; 第二步:如答图 1,在 BE 上取一点 M,使得 ME=CE,连接 DM; 第三步:证明 DM=CF,DM=BD 即可. 【解答】结论:BD=CF. 理由:如答图 1,在 BE 上取一点 M,使得 ME=CE,连接 DM. DE=EF,∠DEM=∠CEF,EM=EC,∴△DEM≌△FEC, ∴DM=CF,∠MDE=∠F, ∴DM∥CF,∴∠BDM=∠BAC=90°. AB=AC,∴∠DBM=45°,∴BD=DM,∴BD=CF. (3)若 AB=3,AE= 5,求 BD 的长. 解题思路 第一步:如答图 2,过点 E 作 EN⊥AD 交 AD 于点 N; 第二...