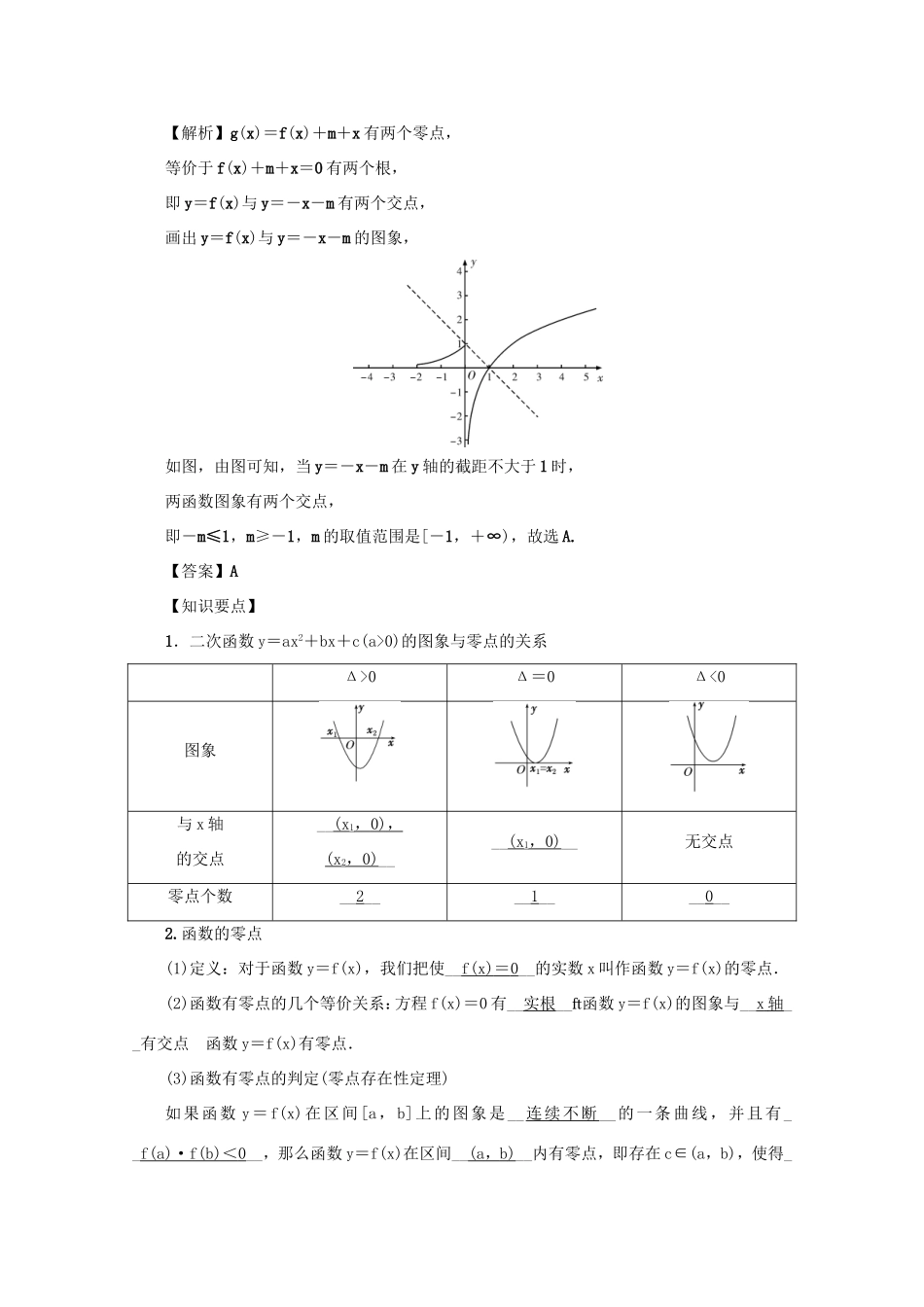
第13讲函数与方程夯实基础【p32】【学习目标】1.结合二次函数的图象,掌握二次方程根的分布情况;2.理解函数零点的概念和性质,会用二分法求函数的零点.【基础检测】1.函数f(x)=2x-8的零点是()A.3B.(3,0)C.4D.(4,0)【解析】函数f(x)的零点等价于方程f(x)=0的根,即2x-8=0,x=3,故选A.【答案】A2.若方程x2+ax+a=0的一根小于-2,另一根大于-2,则实数a的取值范围是()A.B.C.D.∪【解析】令f=x2+ax+a,方程x2+ax+a=0的一根小于-2,另一根大于-2,则f=4-2a+a=4-a<0,解得a>4.故选A.【答案】A3.函数f=x-的零点个数为()A.0B.1C.2D.3【解析】在同一直角坐标系下作出函数y=x与y=的图象,如图所示,由图知,两个函数只有一个交点,所以函数f(x)的零点只有1个,故选B.【答案】B4.已知f(x)=g(x)=f(x)+x+m,若g(x)存在两个零点,则m的取值范围是()A.[-1,+∞)B.[-1,0)C.[0,+∞)D.[1,+∞)【解析】g(x)=f(x)+m+x有两个零点,等价于f(x)+m+x=0有两个根,即y=f(x)与y=-x-m有两个交点,画出y=f(x)与y=-x-m的图象,如图,由图可知,当y=-x-m在y轴的截距不大于1时,两函数图象有两个交点,即-m≤1,m≥-1,m的取值范围是[-1,+∞),故选A.【答案】A【知识要点】1.二次函数y=ax2+bx+c(a>0)的图象与零点的关系Δ>0Δ=0Δ<0图象与x轴的交点__(x1,0),(x2,0)____(x1,0)__无交点零点个数__2____1____0__2.函数的零点(1)定义:对于函数y=f(x),我们把使__f(x)=0__的实数x叫作函数y=f(x)的零点.(2)函数有零点的几个等价关系:方程f(x)=0有__实根__函数y=f(x)的图象与__x轴__有交点函数y=f(x)有零点.(3)函数有零点的判定(零点存在性定理)如果函数y=f(x)在区间[a,b]上的图象是__连续不断__的一条曲线,并且有__f(a)·f(b)<0__,那么函数y=f(x)在区间__(a,b)__内有零点,即存在c∈(a,b),使得__f(c)=0__,这个c也就是方程f(x)=0的__根__.典例剖析【p33】考点1函数零点区间的判定和求解(1)函数f=lnx+x-4的零点所在的区间为()A.B.C.D.【解析】函数f=lnx+x-4,满足f=1+e-4=e-3<0,f=ln3-1>0,由零点存在性定理可知函数f=lnx+x-4的零点所在的区间为.故选C.【答案】C(2)若a0,∴f(1)·f(8)<0,又f(x)=x2-3x-18在区间[1,8]上的图象是连续的,故f(x)=x2-3x-18在区间[1,8]上存在零点.法二:令f(x)=0,得x2-3x-18=0,∴(x-6)(x+3)=0. x=6∈[1,8],x=-3[1,8],∴f(x)=x2-3x-18在区间[1,8]上存在零点.【答案】存在【小结】确定函数f(x)的零点所在区间的2种常用方法:(1)定义法:使用零点存在性定理,函数y=f(x)必须在区间[a,b]上是连续的,当f(a)·f(b)<0时,函数在区间(a,b)内至少有一个零点.(2)图象法:若一个函数(或方程)由两个初等函数的和(或差)构成,则可考虑用图象法求解,如f(x)=g(x)-h(x),作出y=g(x)和y=h(x)的图象,其交点的横坐标即为函数f(x)的零点.考点2函数零点个数的判断和求解(1)函数f=2x-零点的个数为()A.0B.1C.2D.3【解析】在同一直角坐标系下,作出函数y=2x和y=的图象,如图所示.函数f=2x-的零点等价于2x=的根,等价于函数y=2x和y=的交点.由图可知,有一个交点,所以有一个零点.故选B.【答案】B(2)函数f(x)=的零点个数是________.【解析】当x≤0时,f(x)=x2-2,令x2-2=0,得x=(舍)或x=-,即在区间(-∞,0]上,函数只有一个零点.当x>0时,f(x)=2x-6+lnx,令2x-6+lnx=0,得lnx=...