（大纲版）高三数学全程复习方略：第十三章 极限VIP免费

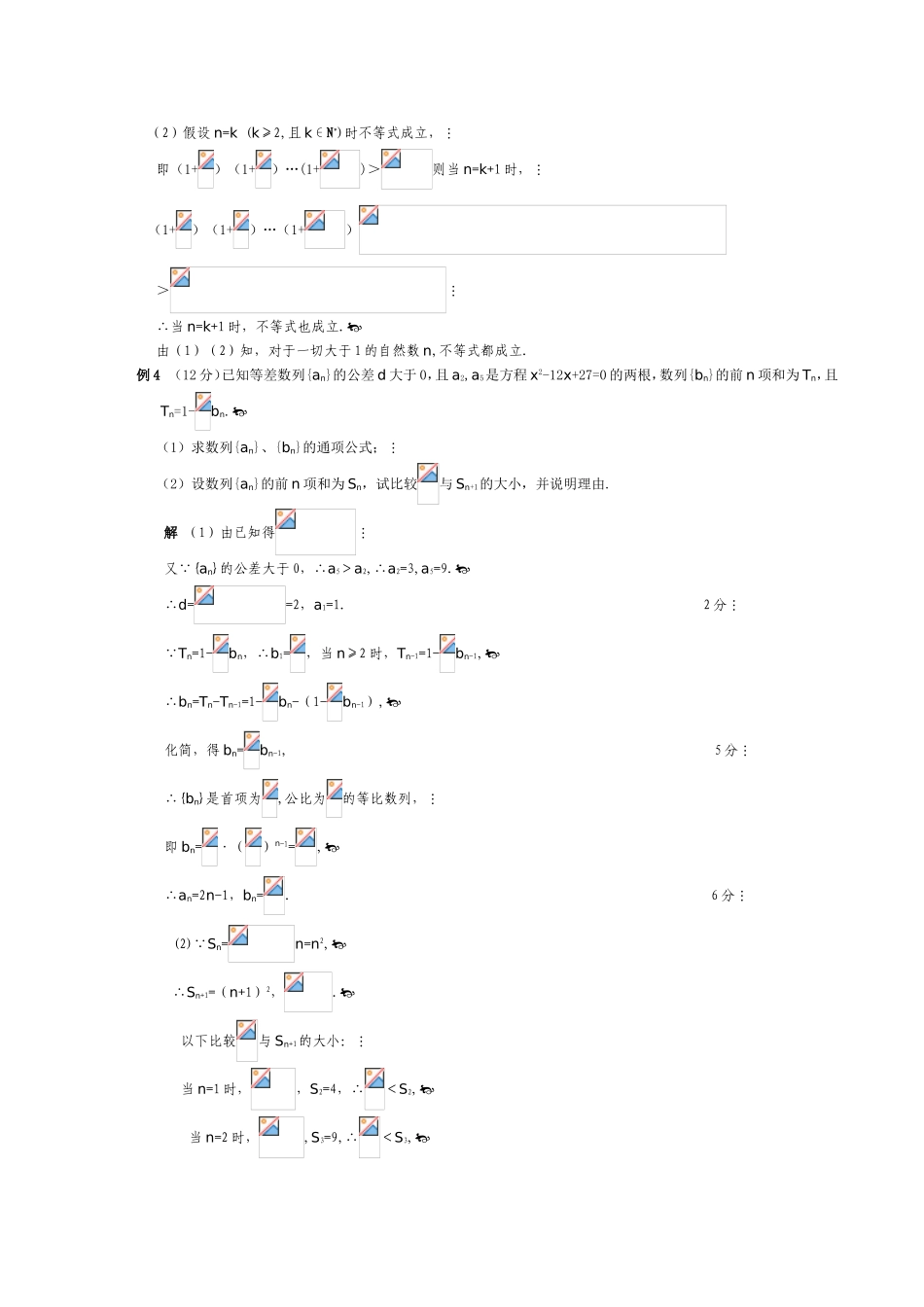
第十三章极限§13.1数学归纳法及其应用基础自测1.用数学归纳法证明：“1+a+a2+…+an+1=(a≠1)”在验证n=1时，左端计算所得的项为（）A.1B.1+aC.1+a+a2D.1+a+a2+a3答案C2.如果命题P（n）对n=k成立，则它对n=k+1也成立，现已知P（n）对n=4不成立，则下列结论正确的是（）A.P（n）对n∈N*成立B.P(n)对n＞4且n∈N*成立C.P（n）对n＜4且n∈N*成立D.P（n）对n≤4且n∈N*不成立答案D3.用数学归纳法证明1+2+3+…+n2=，则当n=k+1时左端应在n=k的基础上加上（）A.k2+1B.(k+1)2C.D.（k2+1）+（k2+2）+（k2+3）+…+（k+1）2答案D4.已知f(n)=++…+，则（）A.f(n)中共有n项，当n=2时，f(2)=B.f(n)中共有n+1项，当n=2时，f(2)=+C.f(n)中共有n2-n项，当n=2时，f(2)=D.f(n)中共有n2-n+1项，当n=2时，f(2)=+答案D5.用数学归纳法证明命题“当n是正奇数时，xn+yn能被x+y整除”，在第二步时，正确的证法是（）A.假设n=k(k∈N*),证明n=k+1命题成立B.假设n=k(k是正奇数)，证明n=k+1命题成立C.假设n=2k+1(k∈N*)，证明n=k+1命题成立D.假设n=k(k是正奇数)，证明n=k+2命题成立答案D例1用数学归纳法证明:时，…+证明（1）当n=1时,左边=右边=左边=右边,所以等式成立.（2）假设n=k(k∈N*)时等式成立,即有…+则当n=k+1时,…+==所以当n=k+1时,等式也成立.由（1）（2）可知,对一切n∈N*等式都成立.例2试证:当n为正整数时，f(n)=32n+2-8n-9能被64整除.证明方法一（1）当n=1时，f(1)=34-8-9=64,命题显然成立.（2）假设当n=k(k≥1,k∈N*)时，f(k)=32k+2-8k-9能被64整除.由于32(k+1)+2-8(k+1)-9=9(32k+2-8k-9)+9·8k+9·9-8(k+1)-9=9(32k+2-8k-9)+64(k+1)即f(k+1)=9f(k)+64(k+1)∴n=k+1时命题也成立.根据（1）（2）可知，对任意的n∈N*，命题都成立.方法二（1）当n=1时，f(1)=34-8-9=64，命题显然成立.（2）假设当n=k(k≥1,k∈N*)时，f(k)=32k+2-8k-9能被64整除.由归纳假设，设32k+2-8k-9=64m(m为大于1的自然数)，将32k+2=64m+8k+9代入到f(k+1)中得f(k+1)=9(64m+8k+9)-8(k+1)-9=64(9m+k+1),∴n=k+1时命题成立.根据（1）（2）可知，对任意的n∈N*，命题都成立.例3用数学归纳法证明：对一切大于1的自然数，不等式（1+）（1+）…（1+）＞均成立.证明（1）当n=2时，左边=1+；右边=. 左边＞右边，∴不等式成立.（2）假设n=k(k≥2,且k∈N*)时不等式成立，即（1+）（1+）…(1+)＞则当n=k+1时，（1+）（1+）…（1+）＞∴当n=k+1时，不等式也成立.由（1）（2）知，对于一切大于1的自然数n,不等式都成立.例4（12分）已知等差数列{an}的公差d大于0，且a2,a5是方程x2-12x+27=0的两根，数列{bn}的前n项和为Tn，且Tn=1-bn.（1）求数列{an}、{bn}的通项公式；（2）设数列{an}的前n项和为Sn，试比较与Sn+1的大小，并说明理由.解（1）由已知得又 {an}的公差大于0，∴a5＞a2,∴a2=3,a5=9.∴d==2，a1=1.2分 Tn=1-bn，∴b1=，当n≥2时，Tn-1=1-bn-1,∴bn=Tn-Tn-1=1-bn-（1-bn-1）,化简，得bn=bn-1,5分∴{bn}是首项为,公比为的等比数列，即bn=·（）n-1=,∴an=2n-1，bn=.6分(2) Sn=n=n2,∴Sn+1=（n+1）2，.以下比较与Sn+1的大小：当n=1时，，S2=4，∴＜S2,当n=2时，,S3=9,∴＜S3,当n=3时，=,S4=16,∴＜S4,当n=4时，=,S5=25,∴＞S5.猜想：n≥4时，＞Sn+1.下面用数学归纳法证明：①当n=4时，已证.②假设当n=k(k∈N*,k≥4)时，＞Sk+1,即＞(k+1)2.9分那么,n=k+1时，=3·＞3(k+1)2=3k2+6k+3=(k2+4k+4)+2k2+2k-1＞［(k+1)+1］2=S(k+1)+1,∴n=k+1时，＞Sn+1也成立.11分由①②可知n∈N*,n≥4时，＞Sn+1都成立.综上所述，当n=1,2,3时，＜Sn+1,当n≥4时，＞Sn+1.12分1.用数学归纳法证明：n∈N*时，1-+…++…+.证明（1）当n=1时，左边=1-===右边，∴等式成立.（2）假设当n=k(k≥1,k∈N*)时，等式成立，即1-+…+=+…+.则当n=k+1时,1-+…+=+…+==即当n=k+1时，等式也成立，所以由（1）（2）知对任意的n∈N*等式成立....