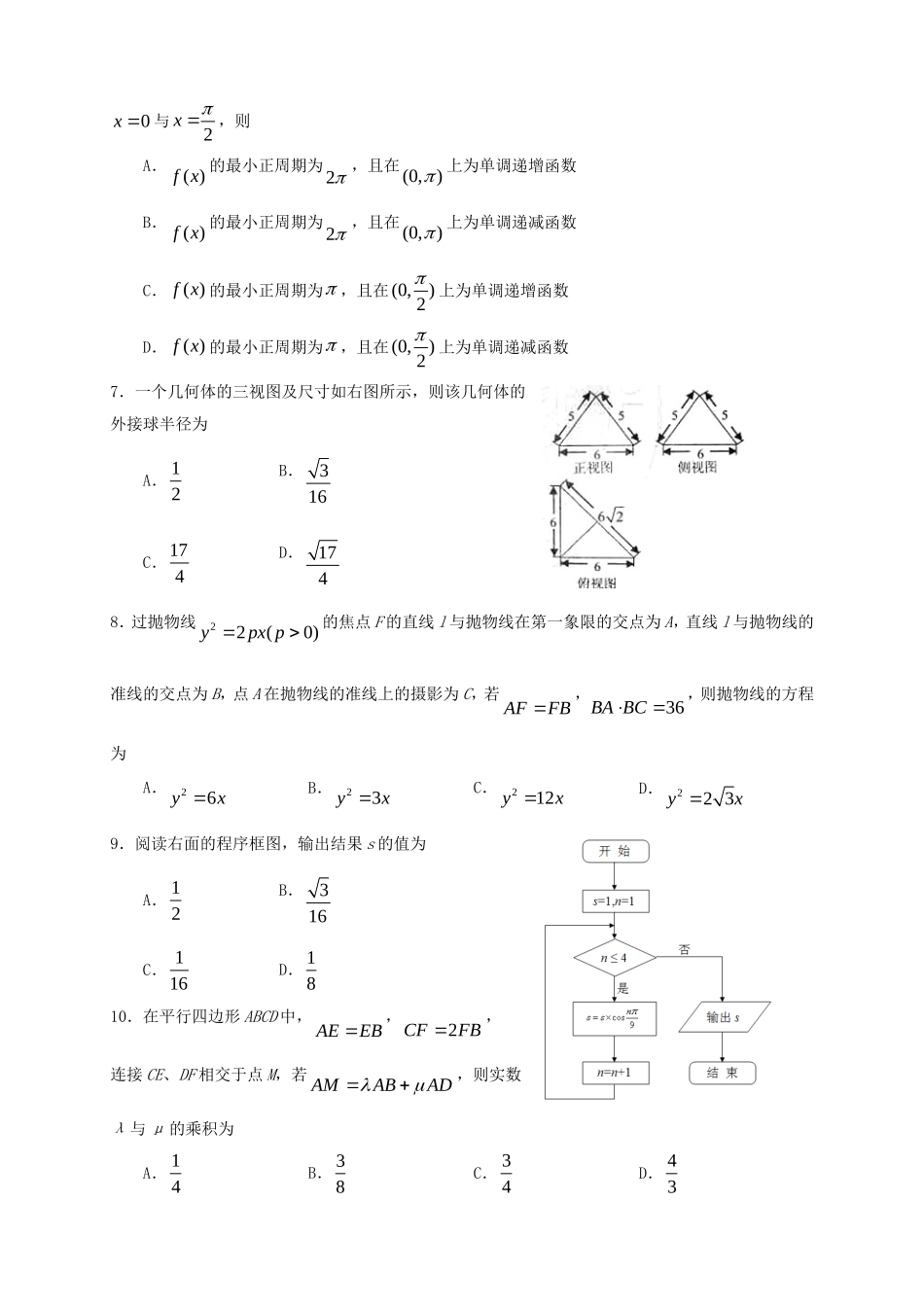
本试卷分为第I卷(选择题)和第II卷(非选择题)两部分,共24题,满分150分,考试时间120分钟。注意事项1.答题前,考生先将自己的姓名、准考证号码填写清楚;2.选择题必须使用2B铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,字迹清楚。3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效。4.保持卡面清洁,不得折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。第I卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合{||1|2}Axx,1{|39}3xBx,则ABA.(1,2)B.(1,2)C.(1,3)D.(1,3)2.设Sn是公差为(0)dd的无穷等差数列{}na的前n项和,则“d<0”是“数列{}nS有最大项”的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件3.ΔABC中,(cos,sin)mAA,(cos,sin)nBB,若12mn,则角C为A.3B.23C.6D.564.已知11eadxx,则61()xax展开式中的常数项为A.20B.-20C.-15D.155.正三棱柱ABC—A1B1C1的所有棱长都为2,则异面直线AB1与BC1所成角的余弦值为A.12B.14C.23D.646.已知函数()sin()3cos()(0,||)2fxxx,其图象相邻的两条对称轴方程为0x与2x,则A.()fx的最小正周期为2,且在(0,)上为单调递增函数B.()fx的最小正周期为2,且在(0,)上为单调递减函数C.()fx的最小正周期为,且在(0,)2上为单调递增函数D.()fx的最小正周期为,且在(0,)2上为单调递减函数7.一个几何体的三视图及尺寸如右图所示,则该几何体的外接球半径为A.12B.316C.174D.1748.过抛物线22(0)ypxp的焦点F的直线l与抛物线在第一象限的交点为A,直线l与抛物线的准线的交点为B,点A在抛物线的准线上的摄影为C,若AFFB�,36BABC�,则抛物线的方程为A.26yxB.23yxC.212yxD.223yx9.阅读右面的程序框图,输出结果s的值为A.12B.316C.116D.1810.在平行四边形ABCD中,AEEB�,2CFFB�,连接CE、DF相交于点M,若AMABAD�,则实数λ与μ的乘积为A.14B.38C.34D.4311.已知函数32()132xmxmnxy的两个极值点分别为x1,x2,且1(0,1)x,2(1,)x,记分别以m,n为横、纵坐标的点(,)Pmn表示的平面区域为D,若函数log(4)(1)ayxa的图象上存在区域D内的点,则实数a的取值范围为A.(1,3]B.(1,3)C.(3,)D.[3,)12.设点P在曲线xye上,点Q在曲线11(0)yxx上,则||PQ的最小值为A.2(1)2eB.2(1)eC.22D.2第II卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分。将答案填在答题卡的相应位置上。)13.若复数1zi,则zzi__________。14.已知双曲线22221(0,0)xyabab的右焦点为F,由F向其渐近线引垂线,垂足为P,若线段PF的中点在此双曲线上,则此双曲线的离线率为__________。15.已知平面区域Ω=20(,)4yxyyx,直线l:2ymxm和曲线C:24yx有两个不同的交点,直线l与曲线C围城的平面区域为M,向区域Ω内随机投一点A,点A落在区域M内的概率为()PM,若2()[,1]2PM,则实数m的取值范围是__________。16.已知ΔABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1,2cosC+c=2b,则ΔABC的周长的取值范围是__________。三、解答题(本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)已知正项数列满足24(1)nnSa。(1)求数列{}na的通项公式;(2)设11nnnbaa,求数列{}nb的前n项和Tn。18.(本小题满分12分)从某学校高三年级共1000名男生中随机抽取50人测量身高。据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),…,第八组[190,195]。下图是按上述分组方法得到的频率分布直方图的一部分、其中第六组、第七组、第八组人数依次构成等差数列。(1)求第六组、第七...