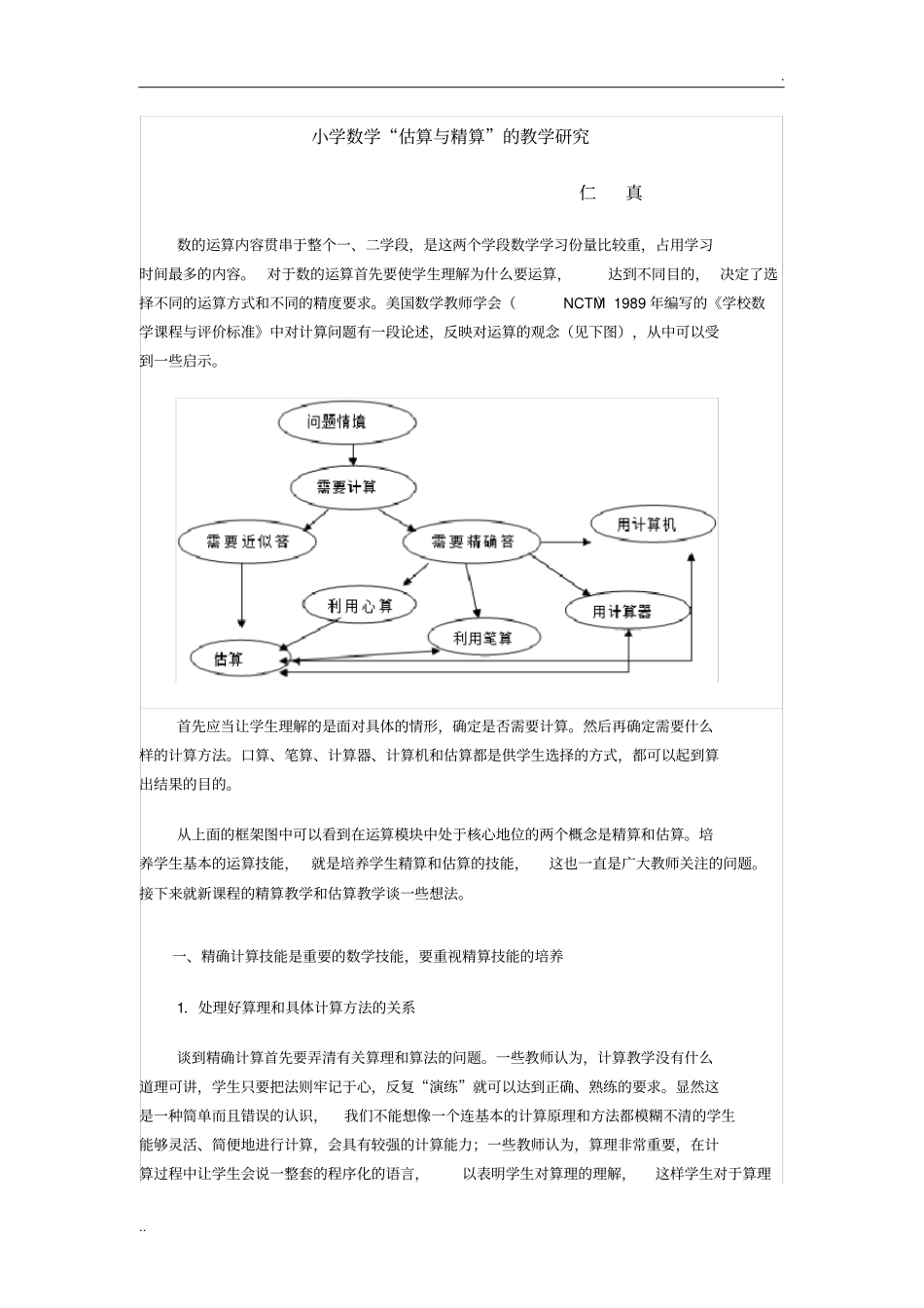
...小学数学“估算与精算”的教学研究仁真数的运算内容贯串于整个一、二学段,是这两个学段数学学习份量比较重,占用学习时间最多的内容。对于数的运算首先要使学生理解为什么要运算,达到不同目的,决定了选择不同的运算方式和不同的精度要求。美国数学教师学会(NCTM)1989年编写的《学校数学课程与评价标准》中对计算问题有一段论述,反映对运算的观念(见下图),从中可以受到一些启示。首先应当让学生理解的是面对具体的情形,确定是否需要计算。然后再确定需要什么样的计算方法。口算、笔算、计算器、计算机和估算都是供学生选择的方式,都可以起到算出结果的目的。从上面的框架图中可以看到在运算模块中处于核心地位的两个概念是精算和估算。培养学生基本的运算技能,就是培养学生精算和估算的技能,这也一直是广大教师关注的问题。接下来就新课程的精算教学和估算教学谈一些想法。一、精确计算技能是重要的数学技能,要重视精算技能的培养1.处理好算理和具体计算方法的关系谈到精确计算首先要弄清有关算理和算法的问题。一些教师认为,计算教学没有什么道理可讲,学生只要把法则牢记于心,反复“演练”就可以达到正确、熟练的要求。显然这是一种简单而且错误的认识,我们不能想像一个连基本的计算原理和方法都模糊不清的学生能够灵活、简便地进行计算,会具有较强的计算能力;一些教师认为,算理非常重要,在计算过程中让学生会说一整套的程序化的语言,以表明学生对算理的理解,这样学生对于算理...真的理解了吗?这样的做法也是不可取的。(1)什么是算理和算法?到底什么是算理?什么是算法呢?这两个问题可能是许多老师经常思考,但却很少追根溯源,有的认识是浅显的,有的甚至是错误的。计算中根据小数的意义,并利用乘法的交换律与结合律,保证了计算结果的正确性,这才是算理。而运算法则是人们进行计算的一个基本程序或方法,它是具有操作性的,先做什么,再做什么,最后做什么。算理是四则运算的理论依据,它是由数学概念、运算定律、运算性质等构成的;具体的计算方法(主要指计算法则)是四则运算的基本程序和方法。运算是基于法则进行的,而法则又要满足运算定律。所以,算理为法则提供理论依据,法则又使算理具体化。(2)教师如何帮助学生理解算理?强调算理的重要性并不难被广大一线老师接受,然而从操作层面如何帮助学生理解算理却是一个棘手且极具技术含量的问题。新课程计算教学淡化了程式化地叙述算理和计算法则,重在让学生经历计算方法的获得过程,重在展示计算方法的形成过程,重在暴露学生的思维过程,让学生真正理解算理,掌握具体的计算方法,形成计算技能。在教学中,既要使学生知道怎么算,又要知道为什么这样算。学生明确了算理和具体的方法,才能灵活、简便地进行计算。在日常教学中我们看到强调算理的重要性并不难被广大一线老师接受,然而从操作层面如何帮助学生理解算理却是一个棘手且极具技术含量的问题。北京小学于萍老师执教的《小数加减法》时,让学生自主进行编题,其中一名学生编出了一道0.8+3.74=,这种类型将要揭示的“小数点对齐”是本节课的重点所在,也是小数加减法总结算法的重要时机。但为了让学生有机会调动已有的整数加减法的认知经验,经历判断、推理、抽象的思维过程,此时老师采取的方式是让每个学生自己试做,并说明自己这样做的道理。小数加减法在小学“数与代数”的学习领域中占有什么位置?如何把握它与整数加减法的关系?在这节课中又该如何呈现知识的本质,抓住核心概念进行教学?于萍老师的教学实践回答了上面的问题。教师在引导学生探究小数加减法计算方法的过程中,始终抓住了本节课知识的“魂”实施教学,她没有满足学生能正确地计算出结果,而是步步深入引导学生逼近数学本质的理解。引发学生对小数加减计算道理的深刻理解,即:小数加减法与整数加减法的本质意义是一致的,即相同的计数单位相加减。像这样,将“讲理”与“明法”有机的结合,让学生在理解算理的基础上总结算法,有助于学生更深入地理解数学核心概念,才能够更好地实现“培养学生根据法则和运算律正确地进行运算的能力。”的目标。...2.直...