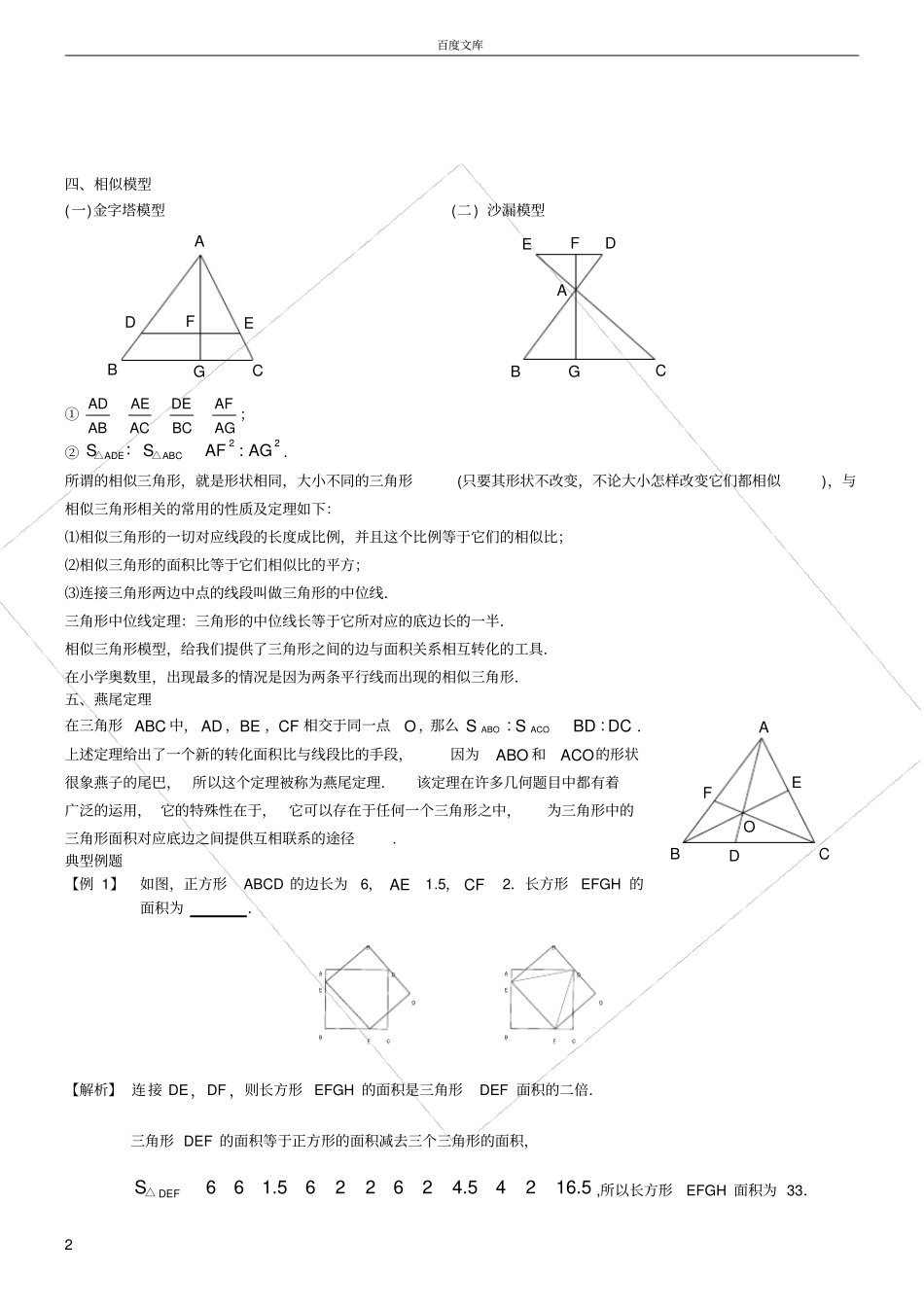
百度文库1小学奥数平面几何五大定律教学目标:1.熟练掌握五大面积模型2.掌握五大面积模型的各种变形知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如右图12::SSab③夹在一组平行线之间的等积变形,如右图ACDBCDSS△△;反之,如果ACDBCDSS△△,则可知直线AB平行于CD.④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC△中,,DE分别是,ABAC上的点如图⑴(或D在BA的延长线上,E在AC上),则:():()ABCADESSABACADAE△△EDCBAEDCBA图⑴图⑵三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①1243::SSSS或者1324SSSS②1243::AOOCSSSS蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝴蝶定理”):①2213::SSab②221324::::::SSSSababab;③S的对应份数为2ab.baS2S1DCBAS4S3S2S1ODCBAABCDObaS3S2S1S4百度文库2四、相似模型(一)金字塔模型(二)沙漏模型GFEABCDABCDEFG①ADAEDEAFABACBCAG;②22:ADEABCSSAFAG△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形.五、燕尾定理在三角形ABC中,AD,BE,CF相交于同一点O,那么::ABOACOSSBDDC.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO和ACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.典型例题【例1】如图,正方形ABCD的边长为6,AE1.5,CF2.长方形EFGH的面积为.【解析】连接DE,DF,则长方形EFGH的面积是三角形DEF面积的二倍.三角形DEF的面积等于正方形的面积减去三个三角形的面积,661.5622624.54216.5DEFS△,所以长方形EFGH面积为33._H_G_F_E_D_C_B_A_A_B_C_D_E_F_G_HOFEDCBA百度文库3【巩固】如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?【解析】本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半.证明:连接AG.(我们通过ABG△把这两个长方形和正方形联系在一起). 在正方形ABCD中,G12ABSABAB△边上的高,∴12ABGABCDSS△(三角形面积等于与它等底等高的平行四边形面积的一半)同理,12ABGEFGBSS△.∴正方形ABCD与长方形EFGB面积相等.长方形的宽88106.4(厘米).【例2】长方形ABCD的面积为362cm,E、F、G为各边中点,H为AD边上任意一点,问阴影部分面积是多少?HGFEDCBA【解析】解法一:寻找可利用的条件,连接BH、HC,如下图:HGFEDCBA可得:12EHBAHBSS、12FHBCHBSS、12DHGDHCSS,而36ABCDAHBCHBCHDSSSS即11()361822EHBBHFDHGAHBCHBCHDSSSSSS;而EHBBHFDHGEBFSSSSS阴影,11111()()364.522228EBFSBEBFABBC.所以阴影部分的面积是:18184.513.5EBFSS阴影解法二:特殊点法.找H的特殊点,把H点与D点重合,那...