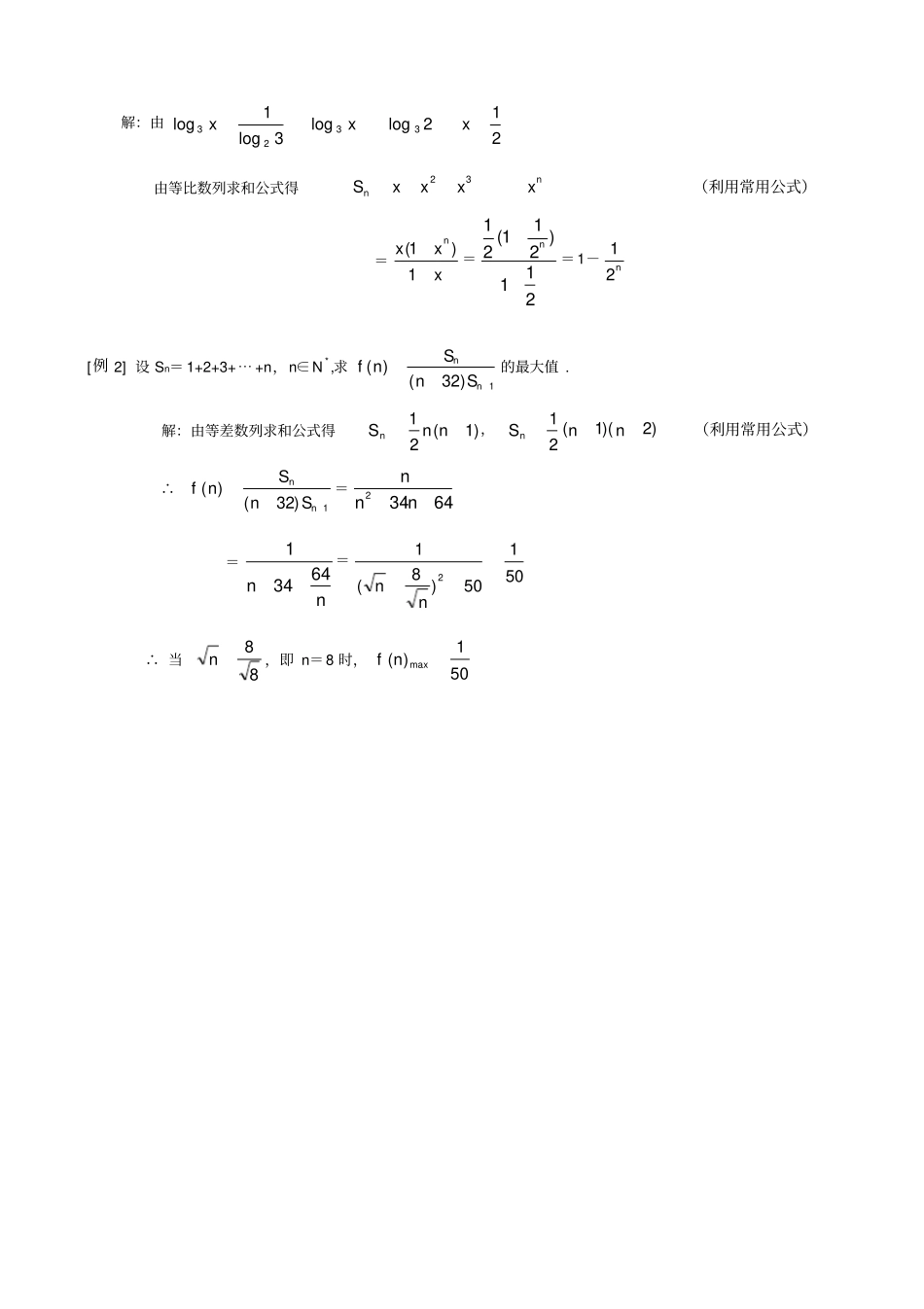
数列求和的基本方法和技巧(配以相应的练习)一、总论:数列求和7种方法:利用等差、等比数列求和公式错位相减法求和反序相加法求和分组相加法求和裂项消去法求和分段求和法(合并法求和)利用数列通项法求和二、等差数列求和的方法是逆序相加法,等比数列的求和方法是错位相减法,三、逆序相加法、错位相减法是数列求和的二个基本方法。数列是高中代数的重要内容,又是学习高等数学的基础.在高考和各种数学竞赛中都占有重要的地位.数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部分数列的求和都需要一定的技巧.下面,就几个历届高考数学和数学竞赛试题来谈谈数列求和的基本方法和技巧.一、利用常用求和公式求和利用下列常用求和公式求和是数列求和的最基本最重要的方法.1、等差数列求和公式:dnnnaaanSnn2)1(2)(112、等比数列求和公式:)1(11)1()1(111qqqaaqqaqnaSnnn3、)1(211nnkSnkn4、)12)(1(6112nnnkSnkn5、213)]1(21[nnkSnkn[例1]已知3log1log23x,求nxxxx32的前n项和.解:由212loglog3log1log3323xxx由等比数列求和公式得nnxxxxS32(利用常用公式)=xxxn1)1(=211)211(21n=1-n21[例2]设Sn=1+2+3+⋯+n,n∈N*,求1)32()(nnSnSnf的最大值.解:由等差数列求和公式得)1(21nnSn,)2)(1(21nnSn(利用常用公式)∴1)32()(nnSnSnf=64342nnn=nn64341=50)8(12nn501∴当88n,即n=8时,501)(maxnf题1.等比数列的前n项和Sn=2n-1,则=题2.若12+22+⋯+(n-1)2=an3+bn2+cn,则a=,b=,c=.解:原式=答案:二、错位相减法求和这种方法是在推导等比数列的前n项和公式时所用的方法,这种方法主要用于求数列{an·bn}的前n项和,其中{an}、{bn}分别是等差数列和等比数列.[例3]求和:132)12(7531nnxnxxxS⋯⋯⋯⋯⋯⋯⋯⋯⋯①解:由题可知,{1)12(nxn}的通项是等差数列{2n-1}的通项与等比数列{1nx}的通项之积设nnxnxxxxxS)12(7531432⋯⋯⋯⋯⋯⋯⋯⋯⋯.②(设制错位)①-②得nnnxnxxxxxSx)12(222221)1(1432(错位相减)再利用等比数列的求和公式得:nnnxnxxxSx)12(1121)1(1∴21)1()1()12()12(xxxnxnSnnn[例4]求数列,22,,26,24,2232nn前n项的和.解:由题可知,{nn22}的通项是等差数列{2n}的通项与等比数列{n21}的通项之积设nnnS2226242232⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯①14322226242221nnnS⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯②(设制错位)①-②得1432222222222222)211(nnnnS(错位相减)1122212nnn∴1224nnnS练习题1已知,求数列{an}的前n项和Sn.答案:练习题2的前n项和为____答案:三、反序相加法求和这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个)(1naa.[例5]求证:nnnnnnnCnCCC2)1()12(53210证明:设nnnnnnCnCCCS)12(53210⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯..①把①式右边倒转过来得0113)12()12(nnnnnnnCCCnCnS(反序)又由mnnmnCC可得nnnnnnnCCCnCnS1103)12()12(⋯⋯⋯⋯..⋯⋯..②①+②得nnnnnnnnnCCCCnS2)1(2))(22(2110(反序相加)∴nnnS2)1([例6]求89sin88sin3sin2sin1sin22222的值解:设89sin88sin3sin2sin1sin22222S⋯⋯⋯⋯.①将①式右边反序得1sin2sin3sin88sin89sin22222S⋯⋯⋯⋯..②(反序)又因为1cossin),90cos(sin22xxxx①+②得(反序相加))89cos89(sin)2cos2(sin)1cos1(sin2222222S=89∴S=题1已知函数(1)证明:;(2)求的值.解:(1)先利用指数的相关性质对函数化简,后证明左边=右边(2)利用第(1)小题已经证明的结论可知,两式相加得:所以.练习、求值:练习。已知xf满足21,xxR,当121xx时,2121xfxf,若nS11210fnnfnfnffNn,,求.nS解答:nS)1(41n.由2121xfxf知只要自变量121xx即成立,又知101111nnn,⋯,则易求.nS四、分组法求和有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可.[例7]求数列的前n项和:231,,71,41,1112naaan,⋯解:设)231()71()41()11(12naaaSnn将其每一项拆开再重新组合得)23741()1111(12naaaSnn(分组)当a=1时,2)13(nnnSn=2)13(nn(分组求和)当1a时,2)13(1111nna...