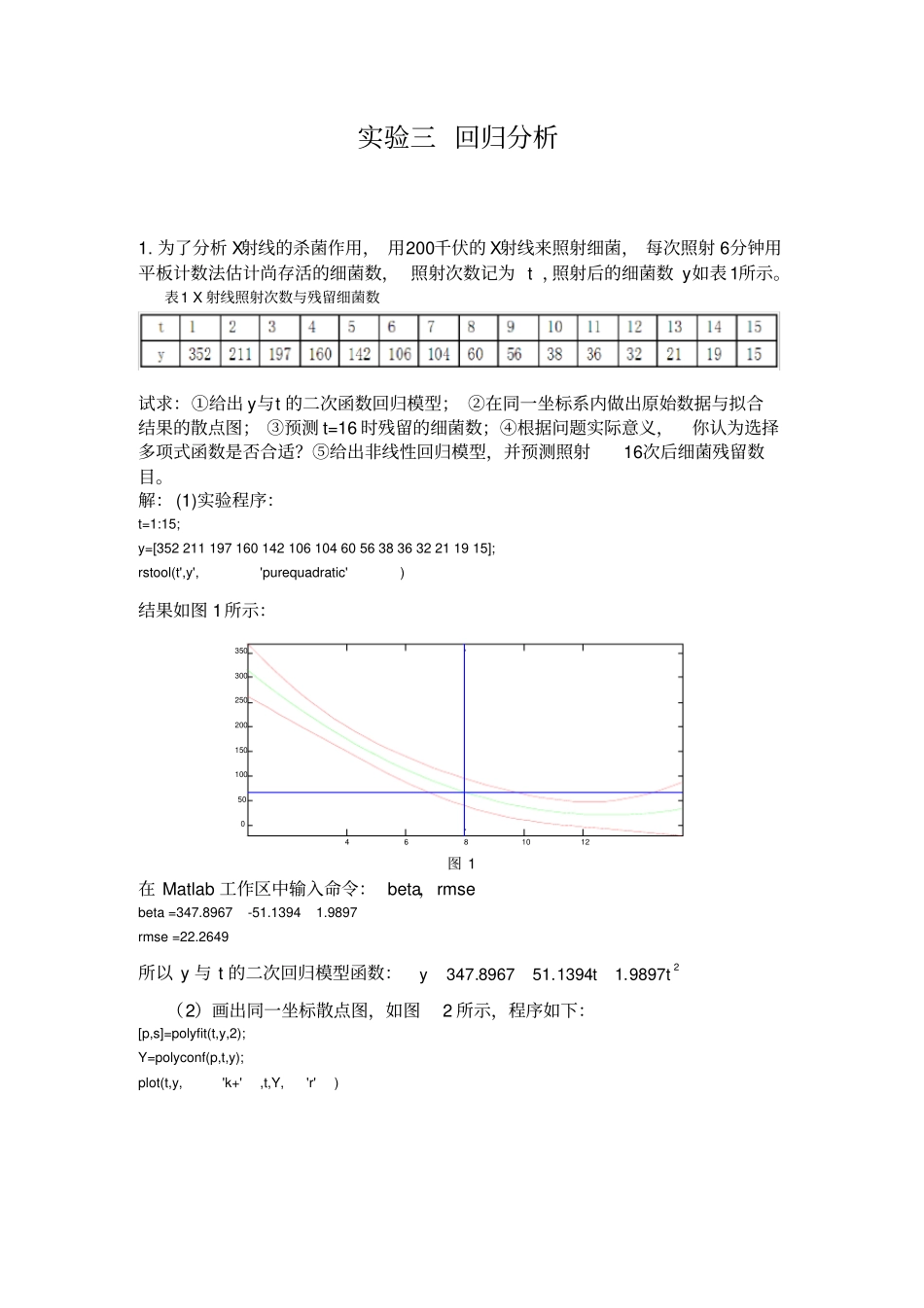
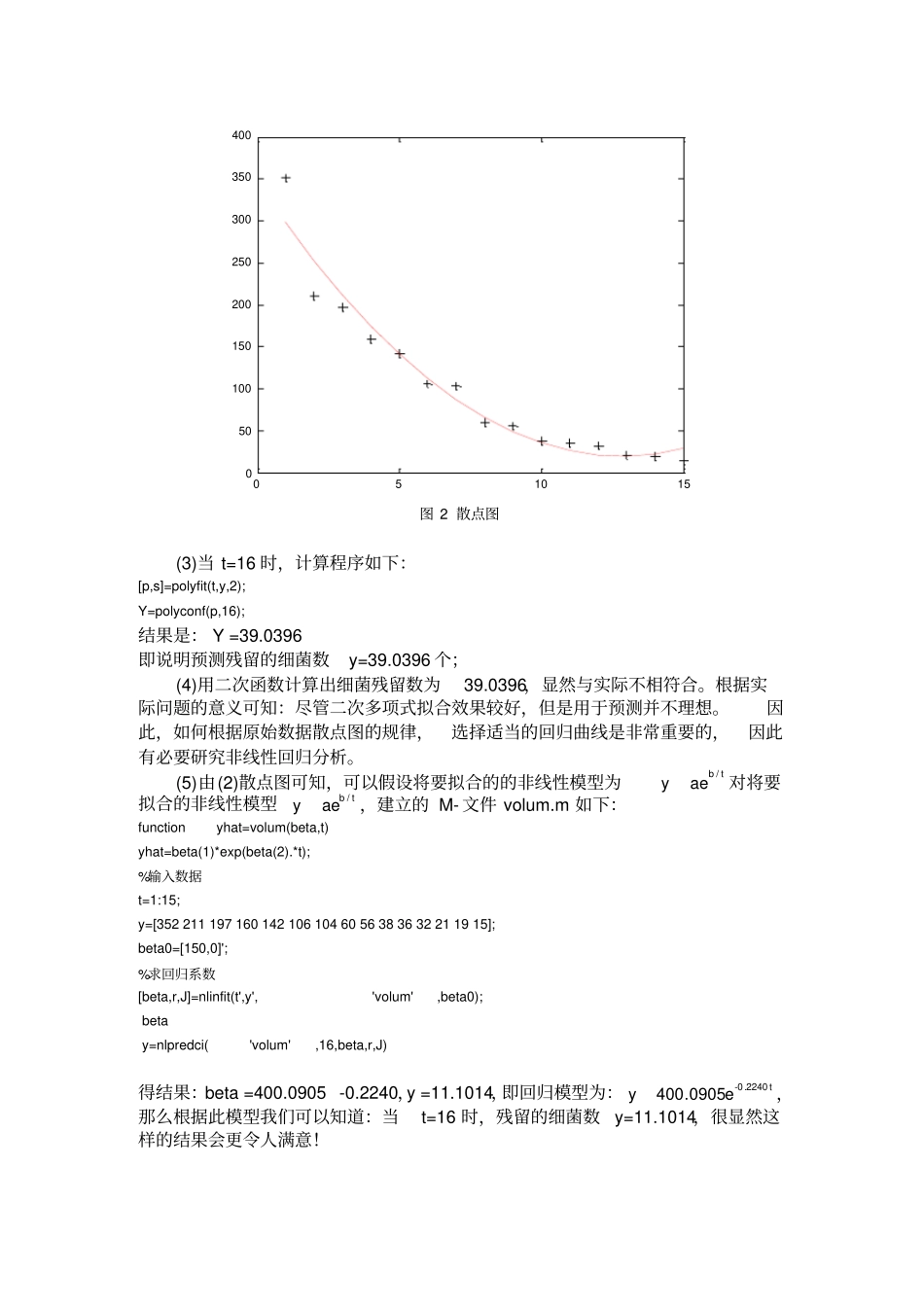
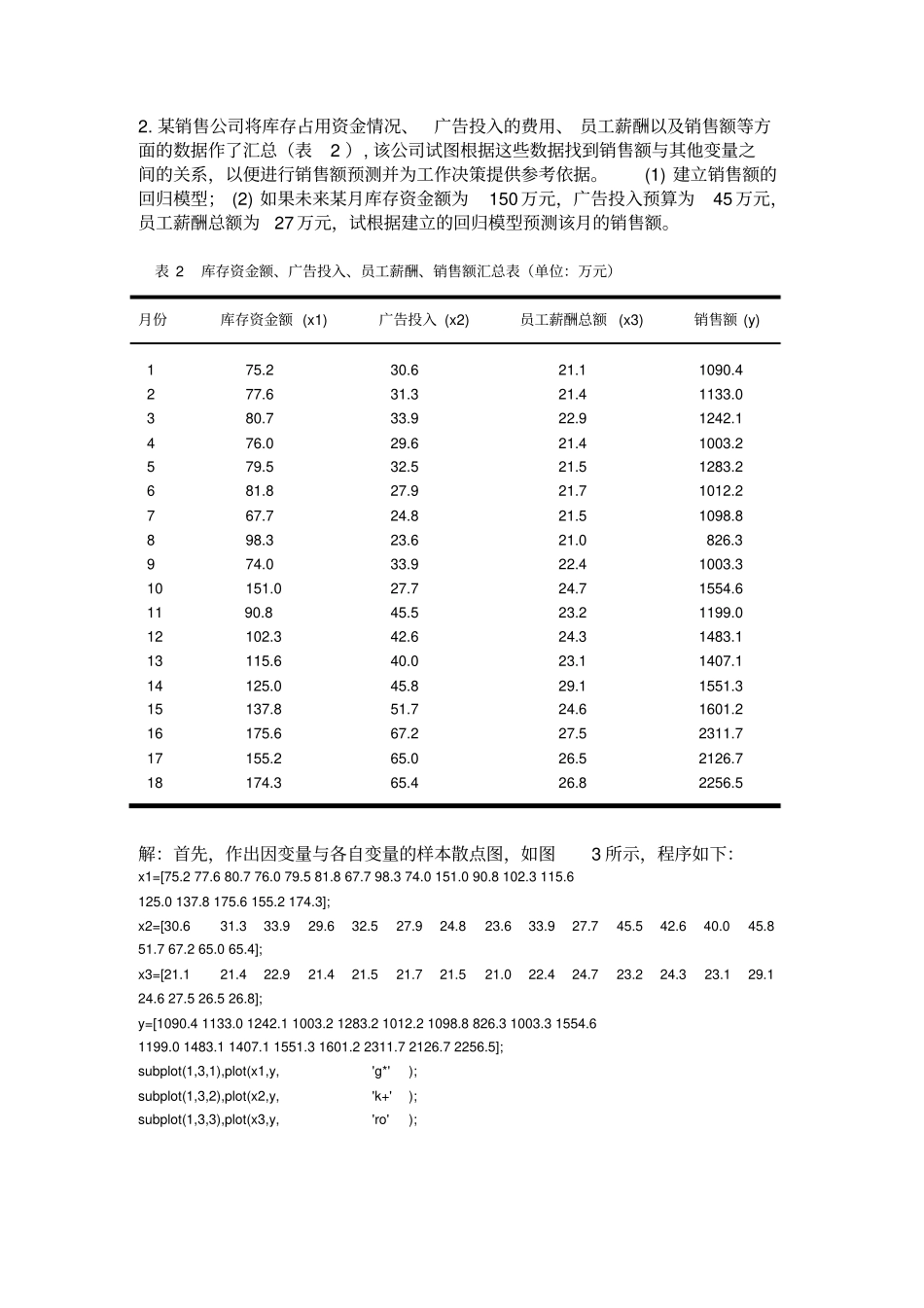
实验三回归分析1.为了分析X射线的杀菌作用,用200千伏的X射线来照射细菌,每次照射6分钟用平板计数法估计尚存活的细菌数,照射次数记为t,照射后的细菌数y如表1所示。表1X射线照射次数与残留细菌数试求:①给出y与t的二次函数回归模型;②在同一坐标系内做出原始数据与拟合结果的散点图;③预测t=16时残留的细菌数;④根据问题实际意义,你认为选择多项式函数是否合适?⑤给出非线性回归模型,并预测照射16次后细菌残留数目。解:(1)实验程序:t=1:15;y=[3522111971601421061046056383632211915];rstool(t',y','purequadratic')结果如图1所示:4681012050100150200250300350图1在Matlab工作区中输入命令:beta,rmsebeta=347.8967-51.13941.9897rmse=22.2649所以y与t的二次回归模型函数:29897.11394.518967.347tty(2)画出同一坐标散点图,如图2所示,程序如下:[p,s]=polyfit(t,y,2);Y=polyconf(p,t,y);plot(t,y,'k+',t,Y,'r')051015050100150200250300350400图2散点图(3)当t=16时,计算程序如下:[p,s]=polyfit(t,y,2);Y=polyconf(p,16);结果是:Y=39.0396即说明预测残留的细菌数y=39.0396个;(4)用二次函数计算出细菌残留数为39.0396,显然与实际不相符合。根据实际问题的意义可知:尽管二次多项式拟合效果较好,但是用于预测并不理想。因此,如何根据原始数据散点图的规律,选择适当的回归曲线是非常重要的,因此有必要研究非线性回归分析。(5)由(2)散点图可知,可以假设将要拟合的的非线性模型为t/baey对将要拟合的非线性模型t/baey,建立的M-文件volum.m如下:functionyhat=volum(beta,t)yhat=beta(1)*exp(beta(2).*t);%输入数据t=1:15;y=[3522111971601421061046056383632211915];beta0=[150,0]';%求回归系数[beta,r,J]=nlinfit(t',y','volum',beta0);betay=nlpredci('volum',16,beta,r,J)得结果:beta=400.0905-0.2240,y=11.1014,即回归模型为:tey2240.0-0905.400,那么根据此模型我们可以知道:当t=16时,残留的细菌数y=11.1014,很显然这样的结果会更令人满意!2.某销售公司将库存占用资金情况、广告投入的费用、员工薪酬以及销售额等方面的数据作了汇总(表2),该公司试图根据这些数据找到销售额与其他变量之间的关系,以便进行销售额预测并为工作决策提供参考依据。(1)建立销售额的回归模型;(2)如果未来某月库存资金额为150万元,广告投入预算为45万元,员工薪酬总额为27万元,试根据建立的回归模型预测该月的销售额。表2库存资金额、广告投入、员工薪酬、销售额汇总表(单位:万元)月份库存资金额(x1)广告投入(x2)员工薪酬总额(x3)销售额(y)175.2277.6380.7476.0579.5681.8767.7898.3974.010151.01190.812102.313115.614125.015137.816175.617155.218174.3解:首先,作出因变量与各自变量的样本散点图,如图3所示,程序如下:x1=[75.277.680.776.079.581.867.798.374.0151.090.8102.3115.6125.0137.8175.6155.2174.3];x2=[30.631.333.929.632.527.924.823.633.927.745.542.640.045.851.767.265.065.4];x3=[21.121.422.921.421.521.721.521.022.424.723.224.323.129.124.627.526.526.8];y=[1090.41133.01242.11003.21283.21012.21098.8826.31003.31554.61199.01483.11407.11551.31601.22311.72126.72256.5];subplot(1,3,1),plot(x1,y,'g*');subplot(1,3,2),plot(x2,y,'k+');subplot(1,3,3),plot(x3,y,'ro');21.121.422.921.421.521.721.521.022.424.723.224.323.129.124.627.526.526.81090.41133.01242.11003.21283.21012.21098.8826.31003.31554.61199.01483.11407.11551.31601.22311.72126.72256.530.631.333.929.632.527.924.823.633.927.745.542.640.045.851.767.265.065.40100200800100012001400160018002000220024000501008001000120014001600180020002200240020253080010001200140016001800200022002400图3因变量y与各自变量的样本散点图从图上可以看出这些点大致分布在一条直线旁边,因此有较好的线性关系,可以采用线性回归。设回归方程为:3322110?????xxxy,建立M-文件输入如下程序:x1=[75.277.680.776.079.581.867.798.374.0151.090.8102.3115.612...