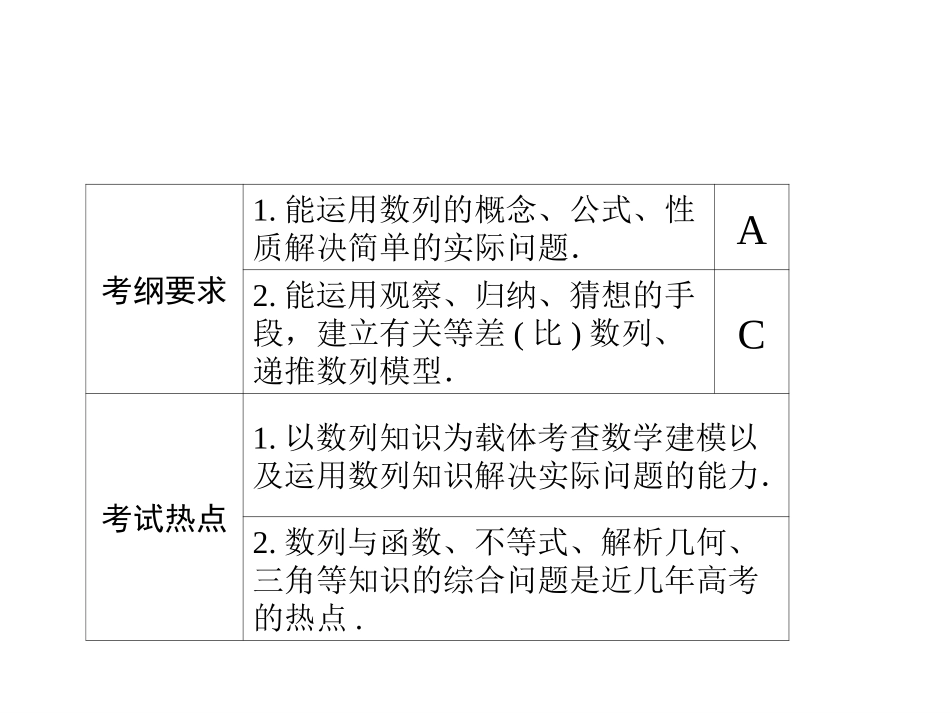
数列的综合运用2014考纲要求1.能运用数列的概念、公式、性质解决简单的实际问题.A2.能运用观察、归纳、猜想的手段,建立有关等差(比)数列、递推数列模型.C考试热点1.以数列知识为载体考查数学建模以及运用数列知识解决实际问题的能力.2.数列与函数、不等式、解析几何、三角等知识的综合问题是近几年高考的热点.高考热点对于本考点,高考重点考查数列通项的求法,与数列有关的不等式的证明以及数列的实际应用题.数列的综合应用一般有四种题型:(1)等差、等比数列的综合题.(2)数列与其他章节知识的综合题:包括数列知识和指数、对数、不等式、三角函数、解析几何等知识的综合.(3)数列的探索性问题:探索性问题检验学生探索规律的能力,因此是高考热点,这类问题对学生分析问题,解决问题的能力有较高要求.热点回顾(4)数列的实际应用:现实生活中涉及利率,产品利润,工作效率,人口增长,常常考虑用数列知识加以解决.1.某种细菌在培养过程中,每20分钟分裂一次(1个分裂成2个),经过3小时,这种细菌由1个可以繁殖成()A.511个B.512个C.1023个D.1024个解析:由题意知,细菌繁殖过程可以看作一个首项为1,公比为2的等比数列模型,所以a10=a1q9=29=512.故应选B.答案:B2.数列{an}的通项公式是关于x的不等式x2-x