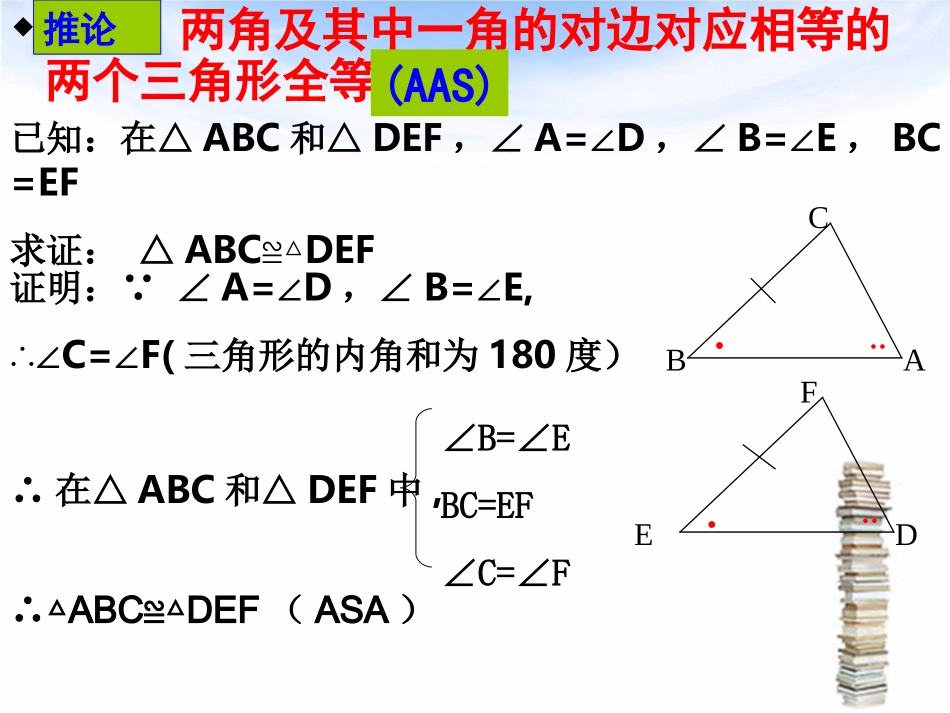
0123450123450123456780123456789109100123456780123456789109100123456780123450123451.1你能证明它们吗(一)1、三角形全等的判定、性质公理判定公理1:三边对应相等的两个三角形全等.(SSS)性质公理:全等三角形的对应边相等、对应角相等.公理2:两边及其夹角对应相等的两个三角形全等.(SAS)公理3:两角及其夹边对应相等的两个三角形全等(ASA)你能用上面的公理证明下面的结论吗?结论:两角及其中一角的对边对应相等的两个三角形全等已知:在△ABC和△DEF,∠A=∠D,∠B=∠E,BC=EF求证:△ABC≌△DEF证明: ∠A=∠D,∠B=∠E,∴∠C=∠F(三角形的内角和为180度)∴在△ABC和△DEF中,∠B=∠EBC=EF∠C=∠F∴△ABCDEF≌△(ASA)BCAEFD●●●●●●证明:两角及其中一角的对边对应相等的两个三角形全等推论(AAS)三角形全等的判定方法判定公理1:(SSS)公理2:(SAS)公理3:(ASA)推论:(AAS)直角三角形(HL)(H代表一条直角边L代表斜边)你还记得吗?1.什么是等腰三角形?2.你会画一个等腰三角形吗?并把你画的等腰三角形裁剪下来。3.试用折纸的办法回忆等腰三角形有哪些性质?2024年11月30日6等腰三角形的性质等腰三角形的性质————验证与证明验证与证明议一议议一议(1)(1)你还记得我们探索过的等腰三角形你还记得我们探索过的等腰三角形的性质吗?的性质吗?ABC底边底边腰腰腰腰顶角底角底角底角底角等腰三角形的两个底角相等等腰三角形的两个底角相等简称简称::等边对等角等边对等角等腰三角形的性质等腰三角形的性质验证方法验证方法用折纸重叠法用折纸重叠法..ABC以底边的中线为折痕以底边的中线为折痕2024年11月30日7““等边对等角”等边对等角”————由实验到论证由实验到论证议一议议一议ABC(2)(2)你能利用已有的公理和定理你能利用已有的公理和定理来证明“等边对等角”这一结论吗来证明“等边对等角”这一结论吗??A把折好的纸打开把折好的纸打开BC不难发现折痕两旁的的两个三角形全等。不难发现折痕两旁的的两个三角形全等。由此实验得到启发——折痕就是由此实验得到启发——折痕就是我们用于证明时要我们用于证明时要添加添加的的辅助线辅助线。。做一做你现在能证明“等边对等角”这一结论吗?你现在能证明“等边对等角”这一结论吗?注意注意千万不要忘记书写的基本格式——千万不要忘记书写的基本格式——写“已知”、“求证”和“证写“已知”、“求证”和“证明”。明”。已知:如图,在△ABC中,AB=AC.求证:∠B=∠C你有哪些方法可以证明?证明:等腰三角形的两个底角相等(等边对等角).ABC已知:如图,在△ABC中,AB=AC.求证:∠B=∠C证明1:取BC的中点D,连接AD AB=AC,BD=CD,AD=AD,∴△ABD≌△ACD(SSS)∴∠B=∠C(全等三角形对应角相等)定理:等腰三角形的两个底角相等(等边对等角).ABC 点D是BC的中点∴BD=CDD已知:如图,在△ABC中,AB=AC.求证:∠B=∠C证明2:过A作∠BAC的平分线,交BC于D,则∠DAB=∠DAC,在△ABD和△ACD中, AB=AC,∠DAB=∠DAC,AD=AD,∴△ABD≌△ACD(SAS)∴∠B=∠C(全等三角形对应角相等)定理:等腰三角形的两个底角相等(等边对等角).ABCDAD还具有哪些性质?已知:如图,在△ABC中,AB=AC.求证:∠B=∠C证明3:过A作AD⊥BC于D,则∠BDA=∠ADC=90°,在RT△ABD和RT△ACD中, AB=AC,AD=AD,∴△ABD≌△ACD(HL)∴∠B=∠C(全等三角形对应角相等)定理:等腰三角形的两个底角相等(等边对等角).ABCD根据刚才的证明,你还能得到哪些结论?推论:等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(三线合一). AB=AC,∠1=∠2.∴BD=CD,AD⊥BC.即:若是顶角的平分线则也是底边上的高和中线 AB=AC,BD=CD.∴∠1=∠2,AD⊥BC即:若是底边上的中线也是顶角的平分线和底边上的高 AB=AC,AD⊥BC.∴BD=CD,∠1=∠2即:若是底边上的高也是底边上的中线和顶角的平分线ABCD121.证明:等边三角形的三个角都相等,并且每个角都等于60°.随堂练习随堂练习已知:如图,在△ABC中,AB=AC=BC.求证:∠B=∠C=A=60∠°ABC证明 AB=AC,AB=BC,∴∠B=∠C,A=C∠∠∴∠B=∠C=A∠又 ∠B+∠C+A=180∠°∴∠B=∠C=A=60∠°2.如图,在△...