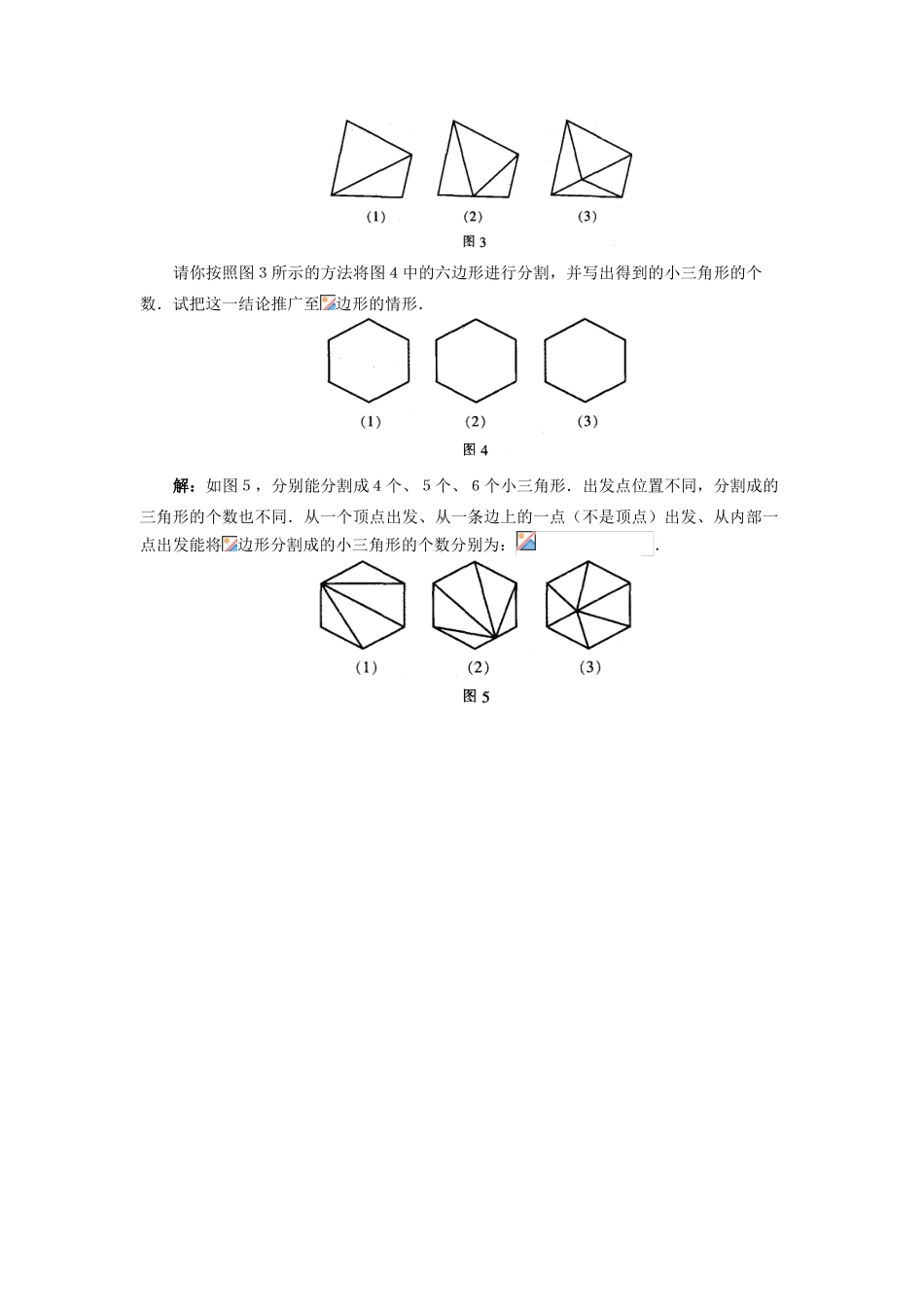
三角形考点综述许建霞本文将“三角形”一章中的主要考点与题型进行总结,帮助同学们进行期中复习.1.三角形的边考试要求:(1)已知三角形两边的长,会利用三角形的三边关系判断第三边的取值范围;(2)能在复杂图形中正确数出三角形的个数.例1在中,,则边的长应满足().A.B.C.D.解:由三角形的三边关系可知应选D.2.三角形的高、中线及角平分线考试要求:(1)会画任意三角形的角平分线、中线和高;(2)能在复杂图形中识别这三种线段.例2如图1,在中,,是边上的高,.图1(1)求的面积.(2)求CD的长.解:(1)∵在中,,∴.(2)因为CD为AB边上的高,所以,即.解得:.注意:求直角三角形的面积一般有两种方法:(1)为两直角边的长);(2)为直角三角形斜边的长,为斜边上的高).由此可知,在四个量中,已知其中三个就可以求出第四个.例3在中,D为BC的中点,则与的面积的大小关系为().A.B.C.D.无法确定解:选C。3.三角形的内角与外角考试要求:会利用三角形的内角和及外角的性质求角的度数.例4如图2,在中,D是AC的延长线上一点,的大小为______.解:因为是的外角,所以图24.多边形及其内角和考试要求:会利用多边形的内角和公式求多边形的内角和及多边形的边数,会利用正多边形进行镶嵌.例5一个多边形的内角和比它的外角和的3倍少,这个多边形的边数是().A.5B.6C.7D.8解:设这个多边形的边数为.由题意,得.解得.故选C.例6阅读材料:从多边形的边上或多边形内部的一点与多边形各顶点连线,可将多边形分割成若干个小三角形,图3给出了四边形的分割方法,分别将四边形分割成了2个、3个、4个小三角形.请你按照图3所示的方法将图4中的六边形进行分割,并写出得到的小三角形的个数.试把这一结论推广至边形的情形.解:如图5,分别能分割成4个、5个、6个小三角形.出发点位置不同,分割成的三角形的个数也不同.从一个顶点出发、从一条边上的一点(不是顶点)出发、从内部一点出发能将边形分割成的小三角形的个数分别为:.