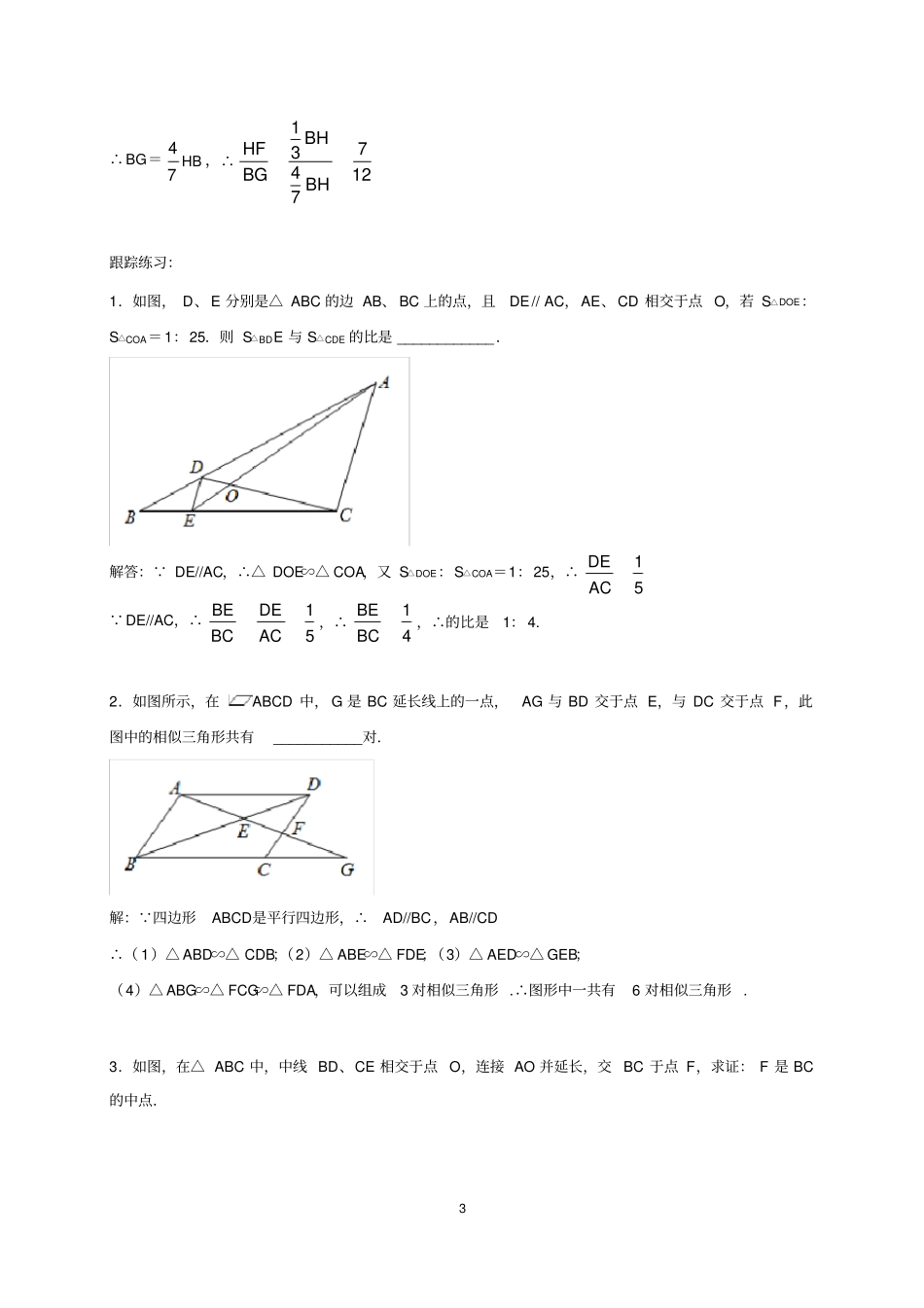
1相似模型模型1:A、8模型已知∠1=∠2结论:△ADE∽△ABC模型分析如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.在做题使,我们也常常关注题目由平行线所产生的相似三角形.模型实例【例1】如图,在ABC中,中线AF、BD、CE相交于点O,求证:12OFOEODOAOCOB.解答:证法一:如图①,连接DE. D、E是中点,∴12DEBC.,DE//BC2∴△EOD∽△COB(8模型)∴12OEDEOCBC.同理:12OFOA,12ODOB.∴12OFOEODOAOCOB.证法二:如图②,过F作FG//AC交BD于点G, F是中点,∴12GFBFADBC. AD=CD,∴12GFAD. FG//AD,∴△GOF∽△DOA(8模型)∴12OFGFOAAD.同理12OEOC,12ODOB.∴12OFOEODOAOCOB.【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G,延长BF交CD的延长线于H,若AFDF=2,求HFBG的值.解答: 四边形ABCD是菱形,∴AB=BC=CD=AD.设DF=a,则DF=AE=a,AF=EB=2a. HD//AB,∴△HFD∽△BFA∴12HDDFHFABAFFB,∴HD=1.5a,13FHBH,∴FH=13BH HD//EB,∴△DGH∽△EGB,∴1.5324HGHDaGBEBa,∴47BGHB3∴BG=47HB,∴1734127BHHFBGBH跟踪练习:1.如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,AE、CD相交于点O,若S△DOE:S△COA=1:25.则S△BDE与S△CDE的比是____________.解答: DE//AC,∴△DOE∽△COA,又S△DOE:S△COA=1:25,∴15DEAC DE//AC,∴15BEDEBCAC,∴14BEBC,∴的比是1:4.2.如图所示,在ABCD中,G是BC延长线上的一点,AG与BD交于点E,与DC交于点F,此图中的相似三角形共有___________对.解: 四边形ABCD是平行四边形,∴AD//BC,AB//CD∴(1)△ABD∽△CDB;(2)△ABE∽△FDE;(3)△AED∽△GEB;(4)△ABG∽△FCG∽△FDA,可以组成3对相似三角形.∴图形中一共有6对相似三角形.3.如图,在△ABC中,中线BD、CE相交于点O,连接AO并延长,交BC于点F,求证:F是BC的中点.4证明:连接DE交AF于点G,则DE//BC,DE=12BC,∴G为AF中点∴12EGBF,12EGOEDEFCOCBC,∴BF=FC,即点F是BC的中点4.在△ABC中,AD是角平分线,求证:ABACBDCD.方法一:过点C??CE//AB交AD延长线于点E,∴∠1=∠3,∴△ABD∽△ECD,∴ABBDCECD ∠1=∠2,∴∠2=∠3,AC=CE,∴ABBDACCD方法二:设ABC中BC边上的高为h,则,12ABDSBDhVg,12ACDSCDhVg过D分别作DEAB,于E,DFAC于F,则12ABDSABDEVg,12ACDSACDFVg511221122ABDACDBDhABDESSCDhACDFVVgggg,又 1=2,∴DE=DF,∴ABBDACCD5.如图,△ABC为等腰直角三角形,D是直角边BC的中点,E在AB上,且AE:EB=2:1,求证:CE⊥AD.证明:过点B做BF//AC,交CE延长线于点F,则∠CBF=90°,△AEC∽△BEF AE:EB=2:1,∴BF=12AC=12BC=CD,又AC=CB,∠ACD=∠CBF=90°∴△ACD≌△CBF,∴∠1=∠2, ∠1+∠3=90°,∴∠2+∠3-90°∴∠4=90°,∴CE⊥AD模型2共边共角型已知:∠1=∠2结论:△ACD∽△ABCDACB12模型分析上图中,不仅要熟悉模型,还要熟记模型的结论,有时候题目中会给出三角形边的乘积关系或者比例关系,我们要能快速判断题中的相似三角形,模型中由△ACD∽△ABC进而可以得到:AC2=ADgAB模型实例例1如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B,如果△ABD的面积为15.那么△ACD的面积为.6ACDB解答: ∠DAC=∠B,∠C=∠C,∴△ACD∽△BCA. AB=4,AD=2,∴14ACDABCSS,∴13ACDABDSS, S△ABD=15,∴S△ACD=5例2如图,在Rt△ABC中,∠BAC=90o,AD⊥BC于D.(1)图中有多少对相似三角形?(2)求证:AB2=BDgBC,AC2=CDgCB,AD2=BDgCD(3)求证:ABgAC=BCgADDCBA解答(1)三对.分别是:△ABD∽△CBA;△ACD∽△BCA;△ABD∽△CAD(2) △ABD∽△CBA,∴ABBDBCAB.∴AB2=BDgBC, △ACD∽△BCA∴ACCDCBAC.∴AC2=CDgCB, △ABD∽△CAD,∴ADBDCDAD,∴AD2=BCgCD(3)1122ABCSABACBCADVgg,∴ABgAC=BCgAD跟踪练习:1.如图所示,能判定△ABC∽△DAC的有.①∠B=∠DAC②∠BAC=∠ADC③AC2=DCgBC④AD2=BDgBC7BDCA【答案】①②③2.已知△AMN是等边三角形,∠BAC=120o.求证:(1)AB2=BMgBC;(2)AC2=CNgCB;(3)MN2=BMgNC.CNMBA【答案】证明: ∠BAC=120...