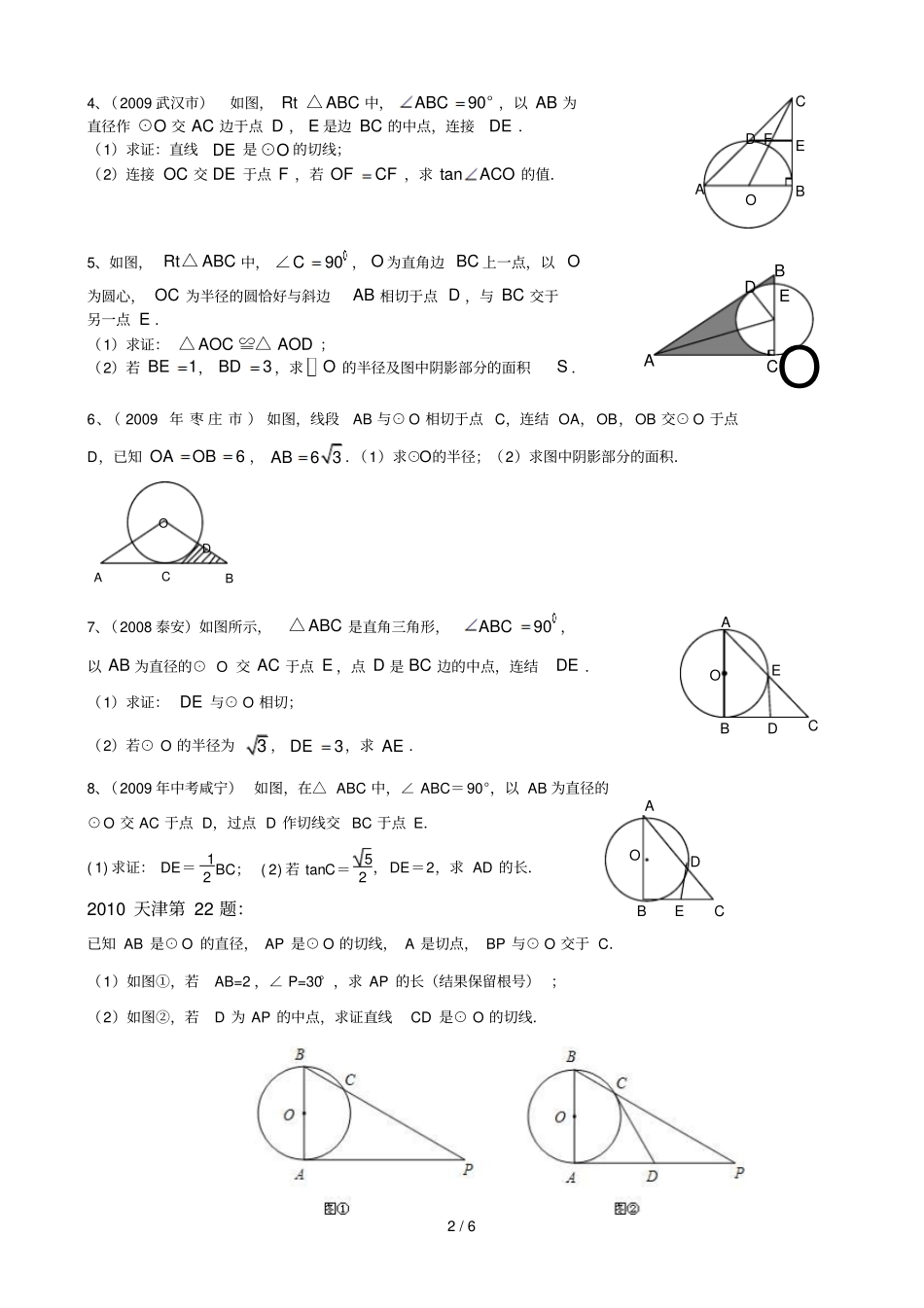
1/6圆的证明和计算题型一:图形主要以圆和三角形(多为等腰三角形或直角三角形)组成;依据所给条件判定圆的切线或已知圆的切线,求图中线段长度或角的度数;主要考查知识有切线的判定、切线的性质、勾股定理、等腰三角形性质、直角三角形性质(斜边中线等于斜边一半、30°所对直角边等于斜边一半等)及解决圆的问题中常加辅助线(已知切线连半径、见直径想直角等)等等。教材原型题:(基本图形为圆和等腰三角形)1、(P45页例1)已知:如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB。求证:直线AB是⊙O的切线。2、(P73页第4题)如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为8cm,AB=10cm,求OA长.3、(P45页练习1)如图,AB是⊙O的直径,∠ABT=45°,AT=AB,求证:AT是⊙O的切线。配套练习:(1、2、3、4题针对原型题1、2;5、6、7、8针对原型题3)1、(2009新疆乌鲁木齐市)如图5,在ABC△中,ABAC,以AB为直径的O⊙交BC于点M,MNAC⊥于点N.(1)求证MN是O⊙的切线;(2)若1202BACAB°,,求图中阴影部分的面积.2、(2009年漳州)如图,点D在O⊙的直径AB的延长线上,点C在O⊙上,ACCD,30D°,(1)求证:CD是O⊙的切线;(2)若O⊙的半径为3,求BC的长.(结果保留π)3、(08福建厦门23题)已知:如图,ABC△中,ABAC,以AB为直径的O交BC于点P,PDAC于点D.(1)求证:PD是O的切线;(2)若1202CABAB,,求BC的值.OCABAOBMNCAOBDCTABOCPBOAD2/6AOBCEDBDCEAO4、(2009武汉市)如图,RtABC△中,90ABC°,以AB为直径作O⊙交AC边于点D,E是边BC的中点,连接DE.(1)求证:直线DE是O⊙的切线;(2)连接OC交DE于点F,若OFCF,求tanACO的值.5、如图,RtABC△中,90C∠,O为直角边BC上一点,以O为圆心,OC为半径的圆恰好与斜边AB相切于点D,与BC交于另一点E.(1)求证:AOCAOD△≌△;(2)若1BE,3BD,求O的半径及图中阴影部分的面积S.6、(2009年枣庄市)如图,线段AB与⊙O相切于点C,连结OA,OB,OB交⊙O于点D,已知6OAOB,63AB.(1)求⊙O的半径;(2)求图中阴影部分的面积.7、(2008泰安)如图所示,ABC△是直角三角形,90ABC,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连结DE.(1)求证:DE与⊙O相切;(2)若⊙O的半径为3,3DE,求AE.8、(2009年中考咸宁)如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D作切线交BC于点E.(1)求证:DE=12BC;(2)若tanC=52,DE=2,求AD的长.2010天津第22题:已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于C.(1)如图①,若AB=2,∠P=30°,求AP的长(结果保留根号);(2)如图②,若D为AP的中点,求证直线CD是⊙O的切线.COABDCEBAOFDACBDEO3/6第23题图OGCABDNMFE题型二:图形是以切线长定理的基本图形所构成;依据所给条件求图中线短长或角的度数;主要考查知识有切线长定理、切线的性质、圆的性质、勾股定理、直角三角形性质及解决圆的问题中常加辅助线等等。教材原型题:1、(P52页第3题)如图,一个钢管放在V形架内,钢管的半径为25cm。(1)如果量得UV=28cm,VT是多少?(2)如果∠UVW=60,VT是多少?2、(P52页第5题)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠BAC=25°,求∠P的度数。3、如图,PA、PB分别切⊙O于点A、B,∠P=70°,则∠C等于()4、(P53页第12题)如图,AB,BC,CD分别是与圆O相切于E,F,G,且AB平行CD,BO等于6cm,CO等于8cm,求BC的长。配套练习:1、(2009年辽宁省朝阳市)如图,O⊙是RtABC△的外接圆,点O在AB上,BDAB,点B是垂足,ODAC∥,连接CD.求证:CD是O⊙的切线.2、(2008湖北省)如图,AB、BC、CD分别与⊙O切于E、F、G,且AB∥CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN∥OB交CD于N.⑴求证:MN是⊙O的切线;⑵当0B=6cm,OC=8cm时,求⊙O的半径及MN的长CABPOTUWVDBAOC(第204/6ADBCEFGO☆3、(2008年潍坊市)如图,AC是圆O的直径,10AC厘米,PAPB,是圆O的切线,AB,为切点.过A作ADBP,交BP于D点,连结ABBC,.(1)求证ABCADB△∽△;(2)若切线AP的长为12厘米,求弦AB的长.☆4、如图,ABAC,是O的两条切线,切点分别为BC,,连结...