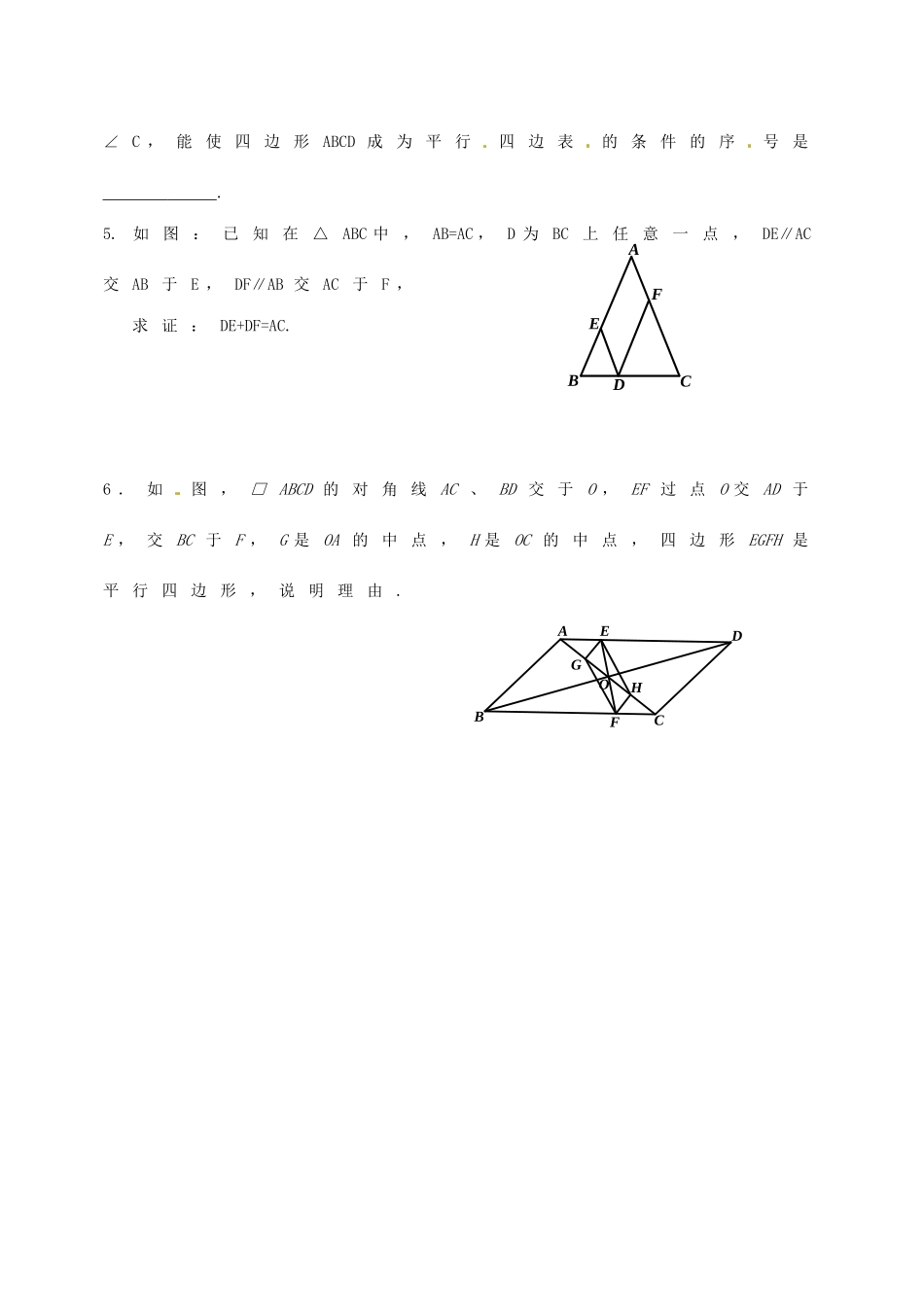
《1.3平行四边形的判定》教学案教学目标:1、会证明平行四边形的判定定理,结合具体命题了解反证法;2、会综合运用平行四边形的判定方法和性质来解决问题,进行简单的计算与证明.教学重点:平行四边形的判定定理教学难点:平行四边形判定的应用,用反证法证明.教学过程:一、引入新课1、我们学过平行四边形的性质有哪些?(从边、角、对角线的角度考察平行四边形的性质)2、平行四边形的判定方法:定义:两组对边分别平行的四边形是平行四边形.定理1:两组对边分别相等的四边形是平行四边形.定理2:一组对边平行且相等的四边形是平行四边形.定理3:对角线互相平分的四边形是平行四边形.二、探索活动问题一:证明:一组对边平行且相等的四边形是平行四边形.问题二:证明:对角线互相平分的四边形是平行四边形.问题三:你认为“在四边形ABCD中,如果OA=OC,OB<OD,那么四边形ABCD不是平行四边形”这个结论正确吗?为什么?反证法:先提出与结论相反的假设,然后由这个“假设”出发推导出矛盾的结果,从而证明命题的结论一定成立.这种证明的方法称为反证法.三、例题1、已知:如图,E、F是平行四边形ABCD的对角线AC上的FABCDEGFOABCDEOABCD两点,AE=CF.求证:四边形BFDE是平行四边形.2、如图,已知E为平行四边形ABCD中DC边的延长线上的一点,且CE=DC,连结AE,分别交BC、BD于点F、G,连结AC交BD于O,连结OF.求证:AB=2OF.四、课堂练习:P201-2五、课堂作业:P268-9六、课堂小结:平行四边形的判定方法,反证法课后作业1.如图,在四边形ABCD中,AC、BD相交于点O,(1)若AD=8cm,AB=4cm,那么当BC=____cm,CD=____cm时,四边形ABCD为平行四边形;(2)若AC=10cm,BD=8cm,那么当AO=___cm,DO=___cm时,四边形ABCD为平行四边形.2.在四边形ABCD中,已知AB∥CD,补充一个条件,使得四边形ABCD是平行四边形.3.若A、B、C是不在同一直线的三点,则以这三点为顶点画平行四边形,可画个.4.已知四边形ABCD中,AD∥BC,分别添加下列条件,①AB∥CD,②AB=DC,③AD=BC,④∠A=∠C,⑤∠B=ABCFDEOABCDEFGH∠C,能使四边形ABCD成为平行四边表的条件的序号是.5.如图:已知在△ABC中,AB=AC,D为BC上任意一点,DE∥AC交AB于E,DF∥AB交AC于F,求证:DE+DF=AC.6.如图,□ABCD的对角线AC、BD交于O,EF过点O交AD于E,交BC于F,G是OA的中点,H是OC的中点,四边形EGFH是平行四边形,说明理由.