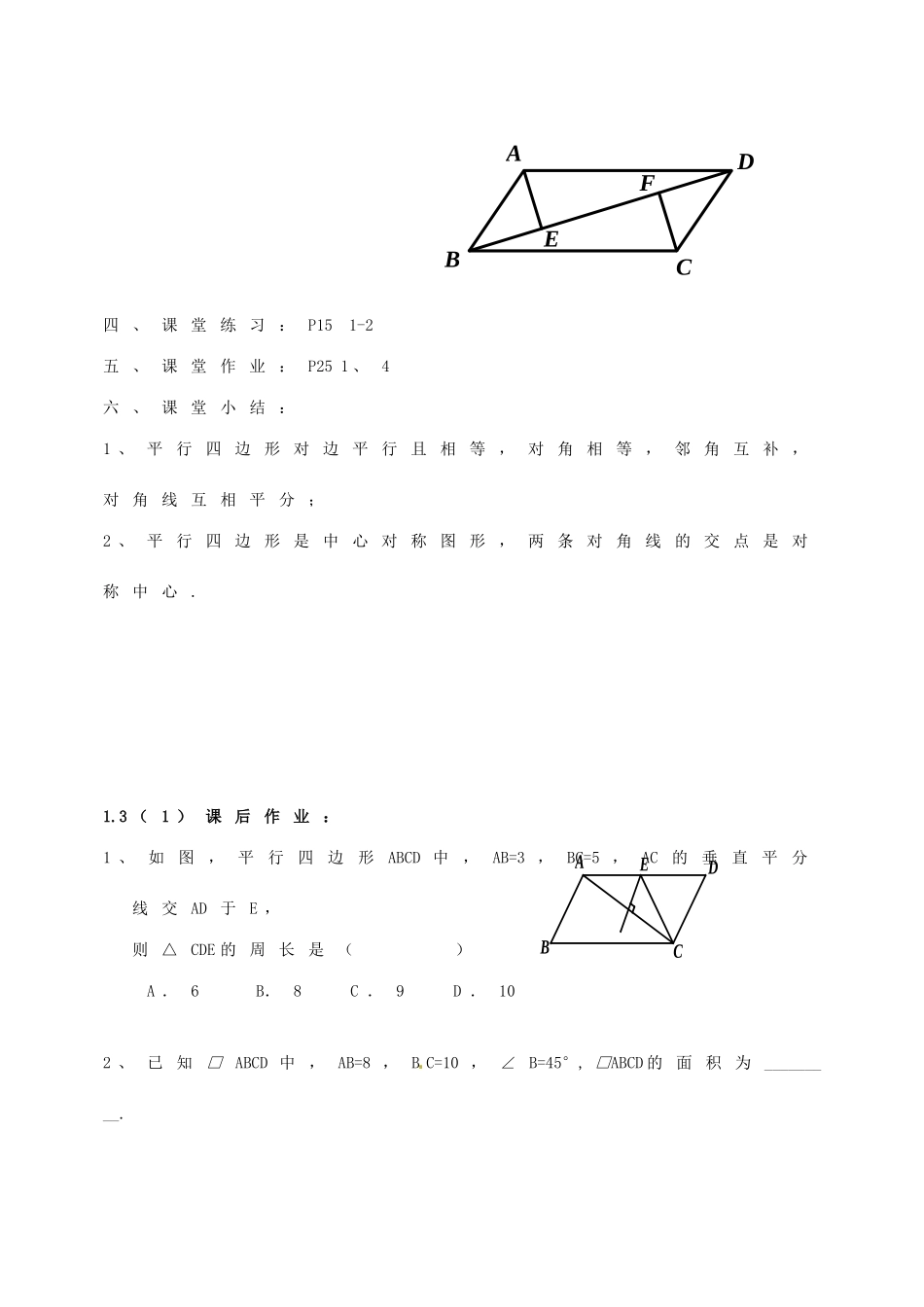
《1.3平行四边形的性质》教学案教学目标:1、会证明平行四边形的性质定理和相关结论.2、能用平行四边形的性质定理进行计算与证明.3、经历探索平行四边形性质的过程,培养学生的动手能力、观察能力及推理能力.教学重难点:平行四边形性质的证明和应用教学过程:一、复习提问:(1)我们学过哪些特殊的四边形?你还记得它们有哪些性质吗?回忆平行四边形、矩形、菱形、正方形的性质,在下表相应的空格内打“√”.平行四边形矩形菱形正方形对边平行对边相等四边相等对角相等4个角是直角对角线互相平分对角线相等对角线互相垂直两条对角线平分两组对角从上面的几种特殊四边形的性质中,你能说说它们之间有什么联系与区别吗?二、探索活动:1、什么样的四边形是平行四边形?(定义)2、平行四边形的三条性质定理:(从边、角、对角线和对称性角度去考虑)平行四边形对边相等;平行四边形对角相等;平行四边形对角线互相平分;平行四边形是中心对称图形,两条对角线的交点是对称中心。你能用基本事实和学过的定理来证明平行四边形的性质吗?三、例题:例1.已知:如图,□ABCD中,E、F分别是AD、BC的中点,求证:BE=DF若将例1中的“E、F分别是AD、BC的中点”改为“AE=AD,CF=BC”,BE与DF相等吗?由此你能得到什么结论?例2.已知:如图,□ABCD中,BD是对角线,AE⊥BD于E,CF⊥BD于F.求证:BE=DF.FEABCDEABCD四、课堂练习:P151-2五、课堂作业:P251、4六、课堂小结:1、平行四边形对边平行且相等,对角相等,邻角互补,对角线互相平分;2、平行四边形是中心对称图形,两条对角线的交点是对称中心.1.3(1)课后作业:1、如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是()A.6B.8C.9D.102、已知□ABCD中,AB=8,BC=10,∠B=45°,□ABCD的面积为_________.3、在△ABC中,AB=AC=5,D是BC上的点,DE∥AB交AC于点E,DF∥AC交AB于点F,那么四边形AFDE的周长是()A.5B.10C.15D.204、□ABCD的周长为50cm,且AB:BC=3:2,则AB=______cm,BC=______cm.5、□ABCD的两条对角线AC与BD交于点O,已知AB=8,BC=6,△AOB的周长为18,则△AOD的周长为_________.6、已知:如图,□ABCD的对角线AC、BD相交于点O,过点O的直线与AD、BC分别相交于点E、F.求证:OE=OF.BDACOEF