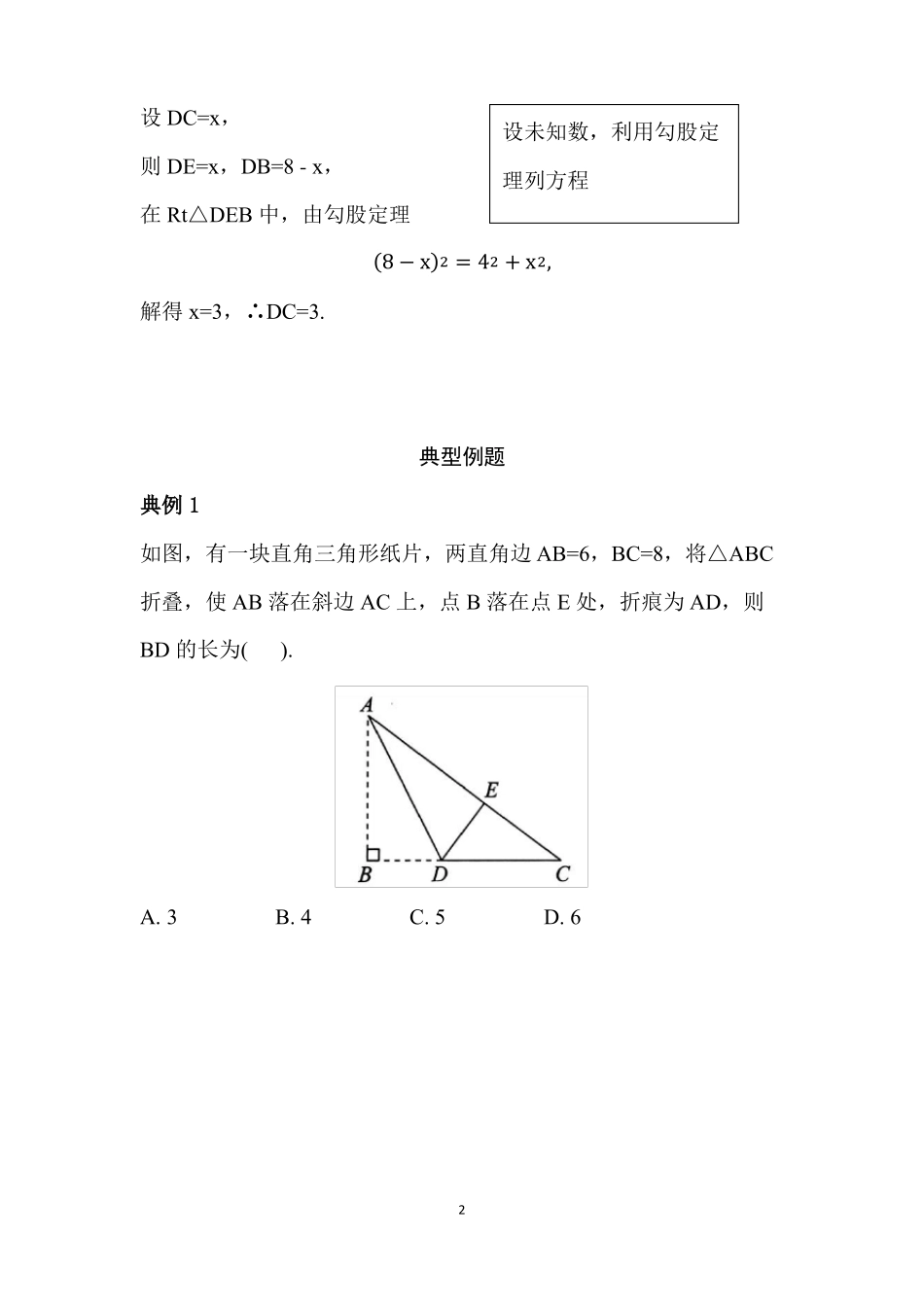
直角三角形锐角平分线模型模型讲解【模型】如图所示,在Rt△ABC中,∠ACB=90°,已知AC=6,BC=8,AD是△ABC的角平分线,求DC的长.【解析】如图,过点D作DE⊥AB,垂足为E,则△ACD≌△AED(AAS),∴AE=AC=6.在Rt△ABC中,由勾股定理得AB=√AC2+BC2=√62+82=10√62+82=10,利用勾股定理求出未知边长易知EB=AB−AE=10−6=4.1设DC=x,则DE=x,DB=8-x,在Rt△DEB中,由勾股定理设未知数,利用勾股定理列方程(8−x)2=42+x2,解得x=3,∴DC=3.典型例题典例1如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,点B落在点E处,折痕为AD,则BD的长为().A.3B.4C.5D.62典例2如图所示,在Rt△ABC中,∠C=90°,AC=8,BC=6,将△BCD沿BD折叠,使点C落在边AB上的点C'处,则折痕BD的长为().A.3√2B.3√3C.3√5D.5√33初露锋芒1.如图所示,有一块直角三角形纸片,∠ACB=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为().A.1cmB.1.5cmC.2cmD.3cm2.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若DE=15cm,BE=8cm,则BC的长为().A.15cmB.17cmC.30cmD.32cm4感受中考1.(2018陕西宝鸡中考模拟)如图所示的三角形纸片中,∠B=90°,AC=13,BC=5.现将纸片进行折叠,使得顶点B落在AC边上的点D处,折痕为AE,则BE的长为().A.2.4B.2.5C.2.85D.3参考答案典型例题典例1【答案】A【解析】∵△ABC为直角三角形,AB=6,BC=8,∴根据勾股定理得AC=√AB2+BC2=10.易知EC=AC-AE=10-6=4.设BD=x,由折叠性质可知DE=BD=x,在Rt△CDE中,根据勾股定理得(8−x)2=42+x2,解得x=3.故选A.典例2【答案】C【解析】∵∠C=90°,AC=8,BC=6,∴AB=10.根据折叠的性质,得BC=BC',CD=DC',易知AC′=AB−C′B=10−6=4.在Rt△AC'D中,设DC'=x,则AD=8-x,根据勾股定理得(8−x)2=x2+42,解得x=3,..CD=3.∴BD=√CD2+BC2=√32+62=3√5.故选C.6初露锋芒1.【答案】A【解析】在Rt△ABC中,AB=√AC2+BC2=√42+32=5(cm),根据折叠的性质可知AE=AB=5cm.∵AC=4cm,∴CE=AE-AC=1cm.即CE的长为1cm.故选A.2.【答案】D【解析】∵AD平分∠CAB,DC⊥AC,DE⊥AB,∴DC=DE=15cm.在Rt△BDE中,BD=√82+152=17(cm)∴BC=CD+BD=15+17=32(cm).故选D.7感受中考1.【答案】A【解析】∵∠B=90°,AC=13,BC=5,∴AB=√AC2−BC2=12.设BE=x,由折叠的性质可得CD=AC-AD=13-12=1,DE=BE=x,∠ADE=∠B=90°,∴EC=BC-BE=5-x.在Rt△DEC中,EC2=CD2+DE2,∴(5−x)2=1+x2,解得x=2.4,∴BE=2.4.故选A.8