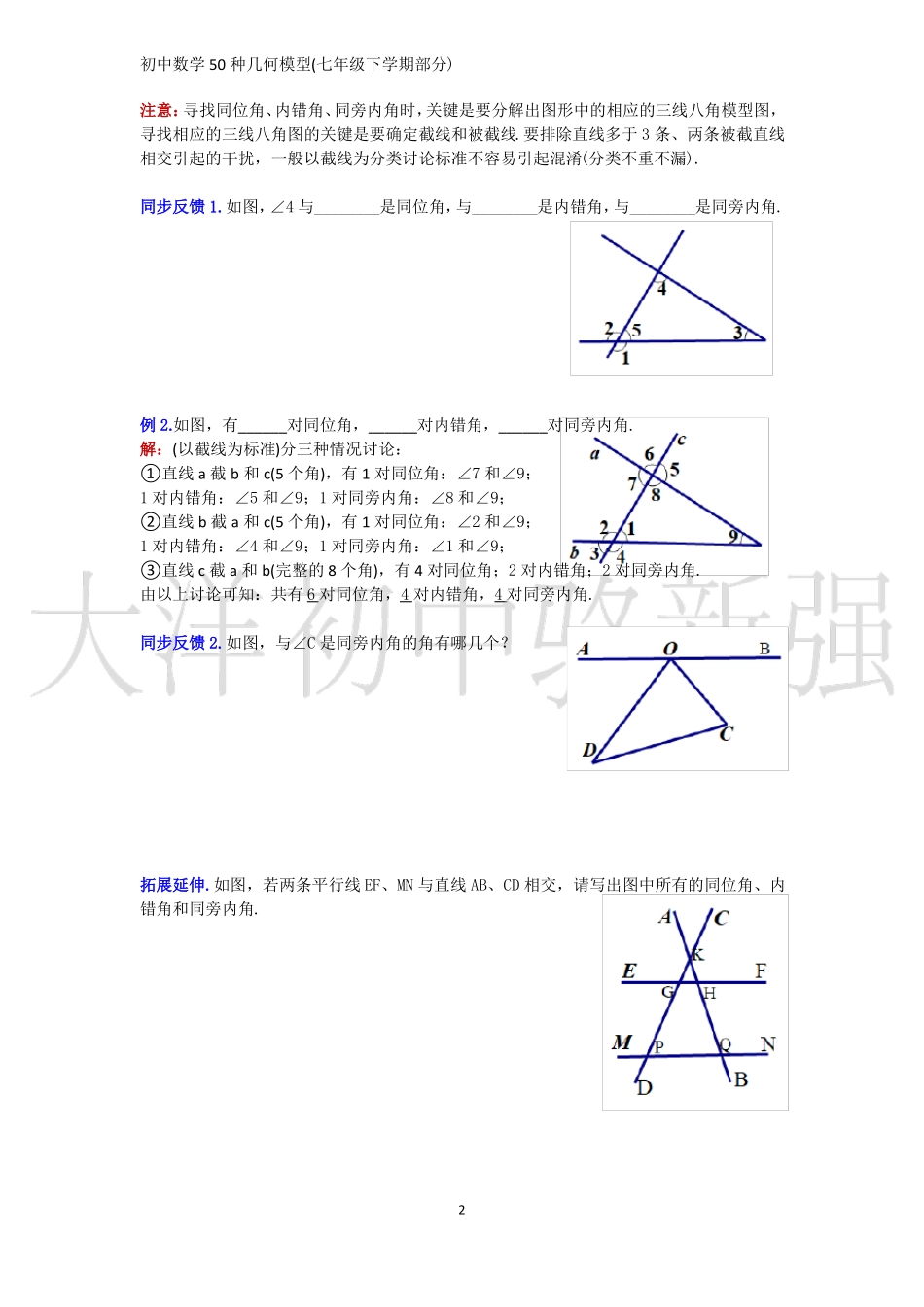
初中数学50种几何模型(七年级下学期部分)二、相交线与平行线§1.三线八角图知识链接如图,两直线被第三条直线所截,所成8个角中,有4对同位角∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8;2对内错角∠3和∠5,∠4和∠6;2对同旁内角∠3和∠6,∠4和∠6.三线八角模型“F”型同位角“Z”型内错角“U”型内错角典例讲解:例1.如图,直线a、b与直线c、d相交.∠1的内错角是______,∠1的同旁内角是______.模型秒杀:∠1由直线a、c相交而成,分两种情况讨论:①若a为截线,截c得∠1,内错角考虑“Z”字型:(如图1)截d得∠2;同旁内角考虑“U”字型:(如图2)截d得∠3;②若c为截线,截a得∠1,内错角考虑“Z”字型:(如图3)截b得∠5;同旁内角考虑“U”字型:(如图4)截b得∠4.由以上讨论可知,∠1的内错角是∠2或∠5,∠1的同旁内角是∠3或∠4.1初中数学50种几何模型(七年级下学期部分)注意:寻找同位角、内错角、同旁内角时,关键是要分解出图形中的相应的三线八角模型图,寻找相应的三线八角图的关键是要确定截线和被截线.要排除直线多于3条、两条被截直线相交引起的干扰,一般以截线为分类讨论标准不容易引起混淆(分类不重不漏).同步反馈1.如图,∠4与________是同位角,与________是内错角,与________是同旁内角.例2.如图,有______对同位角,______对内错角,______对同旁内角.解:(以截线为标准)分三种情况讨论:①直线a截b和c(5个角),有1对同位角:∠7和∠9;1对内错角:∠5和∠9;1对同旁内角:∠8和∠9;②直线b截a和c(5个角),有1对同位角:∠2和∠9;1对内错角:∠4和∠9;1对同旁内角:∠1和∠9;③直线c截a和b(完整的8个角),有4对同位角;2对内错角;2对同旁内角.由以上讨论可知:共有6对同位角,4对内错角,4对同旁内角.同步反馈2.如图,与∠C是同旁内角的角有哪几个?拓展延伸.如图,若两条平行线EF、MN与直线AB、CD相交,请写出图中所有的同位角、内错角和同旁内角.2初中数学50种几何模型(七年级下学期部分)§2.两平行线间的拐点问题(1)知识链接1、平行线的判定:内错角相等,两直线平行; ∠1=∠2,∴a∥b.平行线的性质:两直线平行,内错角相等. a∥b,∴∠1=∠2.2、如图直线AE∥DF,左半边ABOCD象只“猪蹄”,从而我们有以下模型:猪蹄模型(口诀:蹄窝窝是两蹄尖尖的窝)如图1,若AB∥CD,则∠BOC=∠B+∠C.证明:过点O作EF∥AB(如图2),∴∠BOF=∠B(两直线平行,内错角相等). AB∥CD,EF∥AB(已知),∴EF∥CD(平行公理),∴∠COF=∠C(两直线平行,内错角相等).∴∠BOC=∠BOF+∠COF=∠B+∠C.反过来,若∠BOC=∠B+∠C,则AB∥CD.证明:过点O作EF∥AB(如图2),∴∠BOF=∠B(两直线平行,内错角相等).∴∠BOC=∠BOF+∠COF=∠B+∠COF.又 ∠BOC=∠B+∠C,∴∠COF=∠C.∴EF∥CD(内错角相等,两直线平行).∴AB∥CD(平行公理).注意:蹄窝窝是两蹄尖尖的窝,即蹄窝窝∠BOC=两蹄尖尖的和∠B+∠C.选填题可用口诀秒杀,但解答题必须一步一步进行推导,写题过程参考上述两种情况.典例讲解:例1.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=________.模型识别:∠1、∠2组成的图形(如图3)为猪蹄模型.模型秒杀:∠1+∠2=∠BOC=90°.同步反馈1.如图4,在平行线l1、l2之间放置一块直角三角板,三角板的锐角顶点A、B分别在直线l1、l2上,若∠1=65°,则∠2=________.同步反馈2.把一副三角板在水平桌面上如图5摆放,使两个直角顶点重合,两条斜边平行,则∠1==________.3初中数学50种几何模型(七年级下学期部分)例2.如图,∠BCD=90°,AB∥DE,试探索∠1与∠2的数量关系.想题:题中有我们熟悉的猪蹄模型ABCDE,∠ABC+∠2=∠BCD=90°,利用∠ABC=180°-∠1得解.写题如下:解:过点C作CH∥AB(如图2),∴∠ABC=∠BCH(两直线平行,内错角相等). AB∥DE,CH∥AB(已知),∴DE∥CH(平行公理),∴∠2=∠DCH(两直线平行,内错角相等).∴∠ABC+∠2=∠BCH+∠DCH=∠BCD=90°.又 ∠ABC=180°-∠1,∴180°-∠1+∠2=90°.即∠1-∠2=90°.变式1.如图,玲玲在美术课上用丝线绣成了一个“2”,AB∥DE,∠A=30°,∠ACE=110°...