二次方程根的分布情况归纳VIP免费

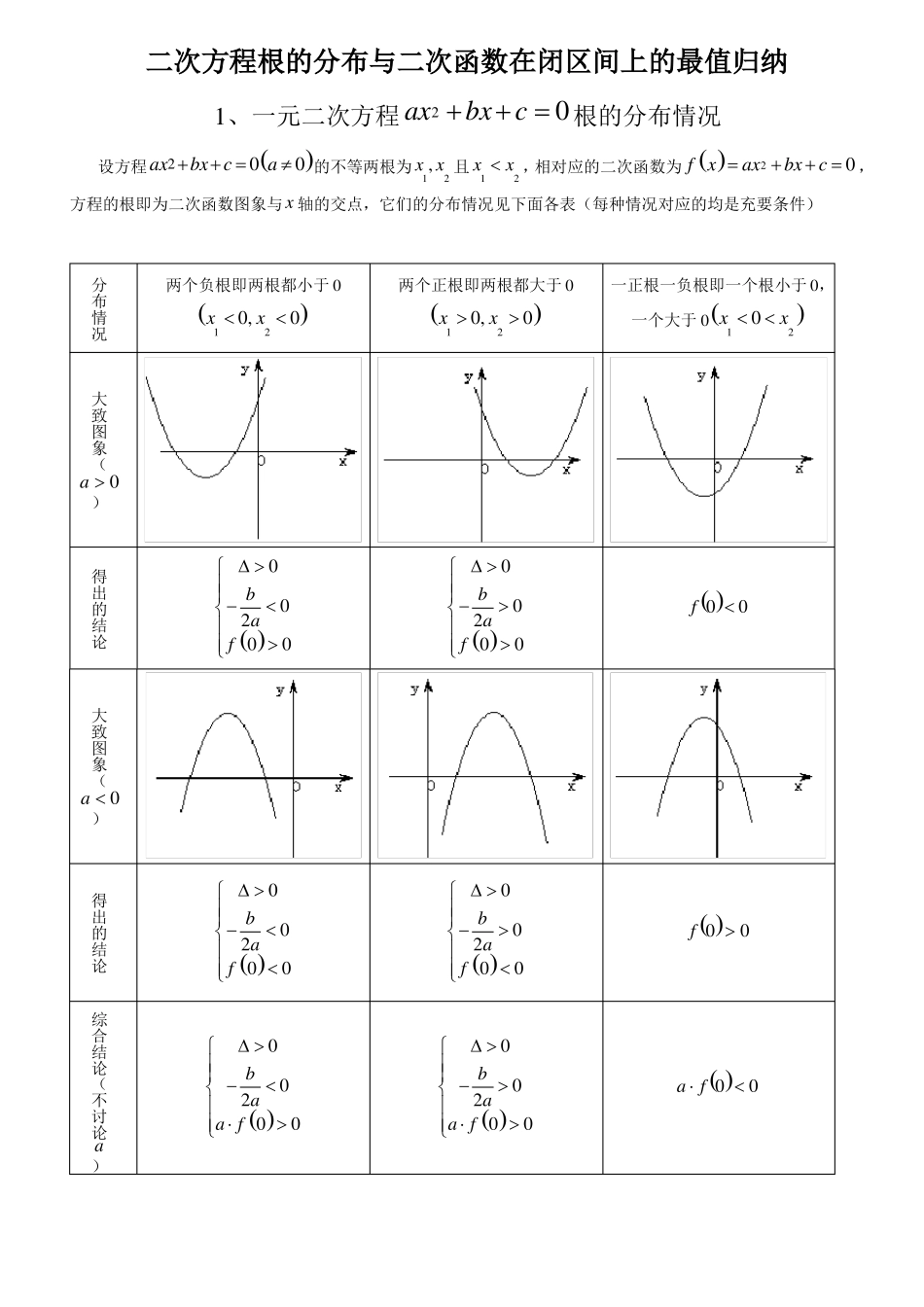
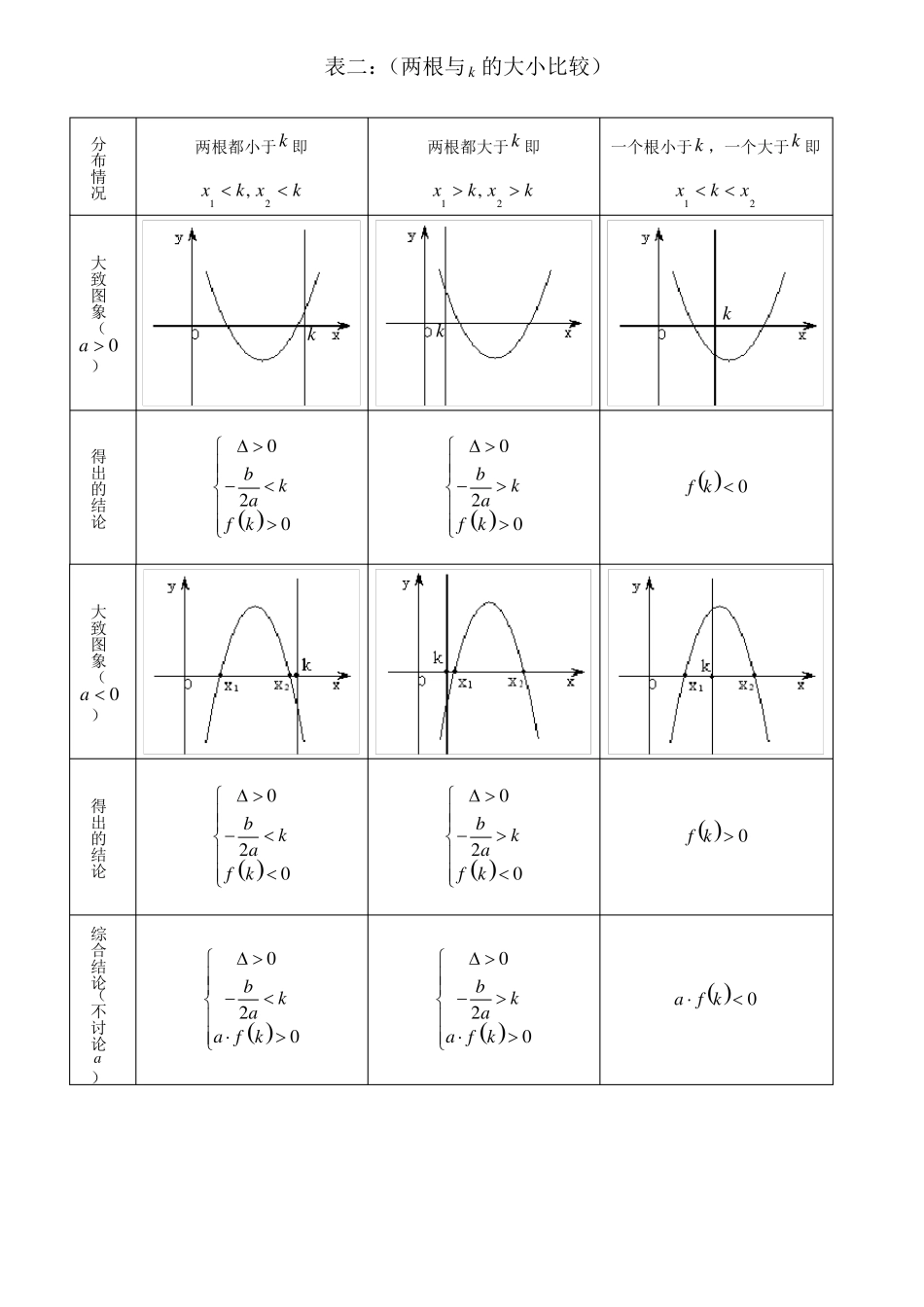
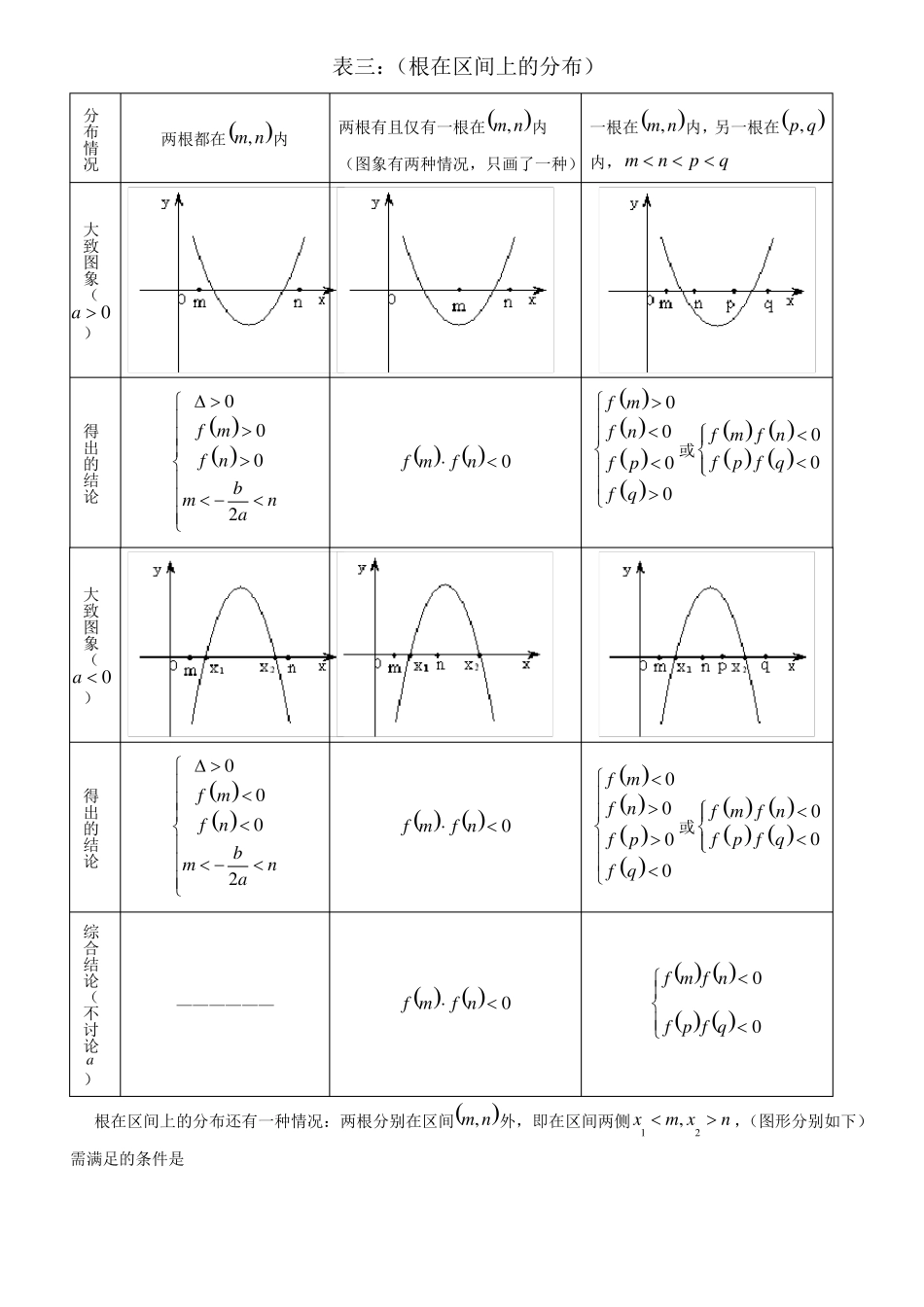
二次方程根的分布与二次函数在闭区间上的最值归纳2axbxc0根的分布情况1、一元二次方程2设方程axbxc0a0的不等两根为x1,x2且x1x2，相对应的二次函数为fxax2bxc0，方程的根即为二次函数图象与x轴的交点，它们的分布情况见下面各表（每种情况对应的均是充要条件）分布情况两个负根即两根都小于0两个正根即两根都大于0一正根一负根即一个根小于0，一个大于0x10x2x10,x20x10,x20a0）a0）大致图象（得出的结论0b02af000b02af00f00大致图象（得出的结论0b02af000b02af00f00综合结论（不讨论a0b02aaf000b02aaf00af00）表二：（两根与k的大小比较）分布情况两根都小于k即两根都大于k即一个根小于k，一个大于k即x1k,x2kx1k,x2kx1kx2a0）a0）大致图象（kkk得出的结论0bk2afk00bk2afk0fk0大致图象（得出的结论0bk2afk00bk2afk0fk0综合结论（不讨论a0bk2aafk00bk2aafk0afk0）表三：（根在区间上的分布）分布情况两根都在m,n内两根有且仅有一根在m,n内一根在m,n内，另一根在p,q（图象有两种情况，只画了一种）内，mnpqa0）a0）需满足的条件是大致图象（得出的结论0fm0fn0bmn2afmfn0fm0fn0fmfn0或fpfq0fp0fq0大致图象（得出的结论0fm0fn0bmn2afmfn0ffffm0n0fmfn0或p0fpfq0q0综合结论（不讨论——————fmfn0fmfn0fpfq0a）根在区间上的分布还有一种情况：两根分别在区间m,n外，即在区间两侧x1m,x2n，（图形分别如下）（1）a0时，fm0fm0；（2）a0时，fn0fn0对以上的根的分布表中一些特殊情况作说明：（1）两根有且仅有一根在m,n内有以下特殊情况：则此时fmfn0不成立，但对于这种情况是知道了方程有一根为m或n，1若fm0或fn0，能够求出另外一根，然后能够根据另一根在区间m,n内，从而能够求出参数的值。如方程mxm2x202在区间1,3上有一根，因为f10，所以mx2m2x2x1mx2，另一根为得22，由13mm2m2即为所求；32方程有且只有一根，且这个根在区间m,n内，即0，此时由0能够求出参数的值，然后再将参数的值带入方程，求出相对应的根，检验根是否在给定的区间内，如若不在，舍去相对应的参数。如方程x24mx2m60有且一根在区间3,0内，求m的取值范围。分析：①由f3f00即1532；②由0即16m42m60得出m1或m，当14233m1时，根x23,0，即m1满足题意；当m时，根x33,0，故m不满足题意；2215综上分析，得出3m或m11414m15m30得出3m根的分布练习题例1、已知二次方程2m1x2mxm10有一正根和一负根，求实数m的取值范围。2解：由2m1f00即2m1m10，从而得1m1即为所求的范围。2例2、已知方程2xm1xm0有两个不等正实根，求实数m的取值范围。2解：由02m18m0m1m322或m3220m122m0m0f000m322或m322即为所求的范围。例3、已知二次函数ym2x22m...