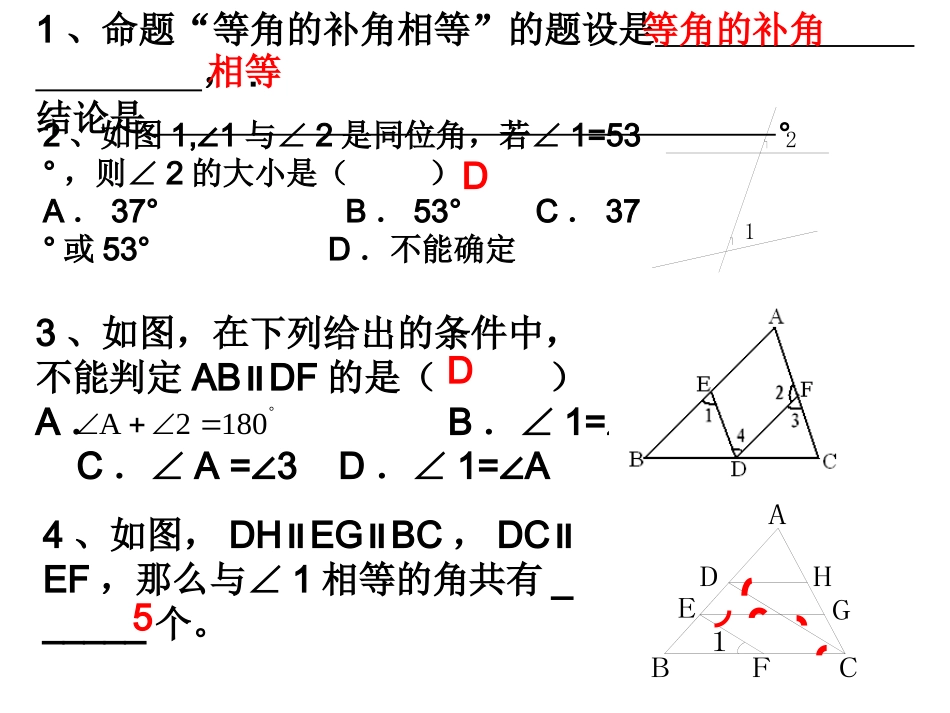
那远去的记忆……平行线强化练习上杭四中林志强1、命题“等角的补角相等”的题设是,.结论是。4、如图,DHEGBC∥∥,DC∥EF,那么与∠1相等的角共有______个。ABFCEDHG13、如图,在下列给出的条件中,不能判定ABDF∥的是()A.B.∠1=4∠C.∠A=3D∠.∠1=A∠1802A2、如图1,1∠与∠2是同位角,若∠1=53°,则∠2的大小是()A.37°B.53°C.37°或53°D.不能确定21等角的补角相等DD52、如图,A、B、C三点在同一直线上,∠1=∠2,∠3=∠D,试说明BD∥CE。作业讲评ABCDE123解:∵∠1=2∠(已知)∴ADBE∥(内错角相等,两直线平行)∴∠D=DBE∠(两直线平行,内错角相等)又∵∠D=3(∠已知)∴∠3=DBE∠∴BDCE∥(等量代换)(内错角相等,两直线平行)如图,ABBF⊥,CDBF⊥,∠1=2∠,试说明∠3=E∠。作业解答ABCDEF123证明:∵ABBF,CDBF⊥⊥∴∠ABD=CDF=90°∠∴ABCD∥∵∠1=2∠∴ABEF∥∴CDEF∥∴∠3=E∠(已知)(垂直定义)(同位角相等,两直线平行)(已知)(内错角相等,两直线平行)(平行于同一直线的两条直线互相平行)(两直线平行,同位角相等)如图EFAD∥,∠1=2∠,∠BAC=70°,求∠AGD的度数。解:∵EFAD∥(已知)∴∠2=3∠又∵∠1=2∠∴∠1=3∠∴DGAB∥∴∠BAC+AGD=180°∴∠AGD=180°-BAC∠=180°-70°=110°(两直线平行,同位角相等)(已知)(等量代换)(内错角相等,两直线平行)(两直线平行,同旁内角互补)如图5-25,∠1+2=180°∠,∠A=∠C,DA平分∠BDF.(1)AE与FC会平行吗?说明理由.(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么.FE21DCBA(1)平行∵∠1+2=180°∠,∠2+CDB=180°∠(邻补角定义)∴∠1=CDB∠∴AEFC∥(同位角相等两直线平行)(2)平行,∵AECF∥,∴∠C=5∠(两直线平行,内错角相等)又∵∠A=C∠∴∠A=5∠∴AFBC∥(两直线平行,内错角相等)(3)平分∵DA平分∠BDF,∴∠3=4∠∵AECF∥,ADBC∥∴∠3=A=5∠∠,∠4=DBC∠∴∠5=DBC∠即BC平分∠DBE345(已知)(角平分线定义)(已知)(?)(?)(等量代换)(角平分线定义)已知DE∥BC,DF、BE分别平分∠ADE和∠ABC求证:∠FDE=∠DEB123证明:∵DE∥BC∴∠ADE=∠ABC()∵DF、BE平分∠ADE、∠ABC∴∠1=∠ADE∠3=∠ABC(角平分线定义)∴∠1=∠3∴DF∥BE()∴∠2=DEB∠()两直线平行,同位角相等1212同位角相等,两直线平行两直线平行,内错角相等(已知)(已知)练习3、如图,∠B+D+BED=360°∠∠,试说明AB∥CD。ABCDE12解:过E作EFAB∥则∠B+1=180°∠∠D+2=180°∠∴∠B+D+BED∠∠=B+D+1+2∠∠∠∠=180°+180°=360°又∵∠BED=1+2∠∠如图,AB∥DE,试问∠B、∠E、∠BCE有什么关系.解:∠B+∠E=∠BCE过点C作CF∥AB,则_______()又∵AB∥DE,AB∥CF,∴____________()∴∠E=∠____()∴∠B+∠E=∠1+∠2即∠B+∠E=∠BCE.CFDE∥平行于同一直线的两条直线互相平行2两直线平行,内错角相等∠B=1∠两直线平行,内错角相等ABCDE12如图,AB∥DE,那么∠B、∠BCD、∠D有什么关系?ABCDEF过C作CFA∥B可得结果:∠B+BCD-∠D=180°∠以上几题有什么共同特点?1,过转折点作平行线2,利用平行线相关性质已知:如图,AB//CD,试解决下列问题:(1)∠1+∠2=______;(2)∠1+∠2+∠3=_____;(3)∠1+∠2+∠3+∠4=_____;(4)试探究∠1+∠2+∠3+∠4+…+∠n=;180°360°540°180°×(n-1)