初中数学几何模型之倍长中线模型VIP免费

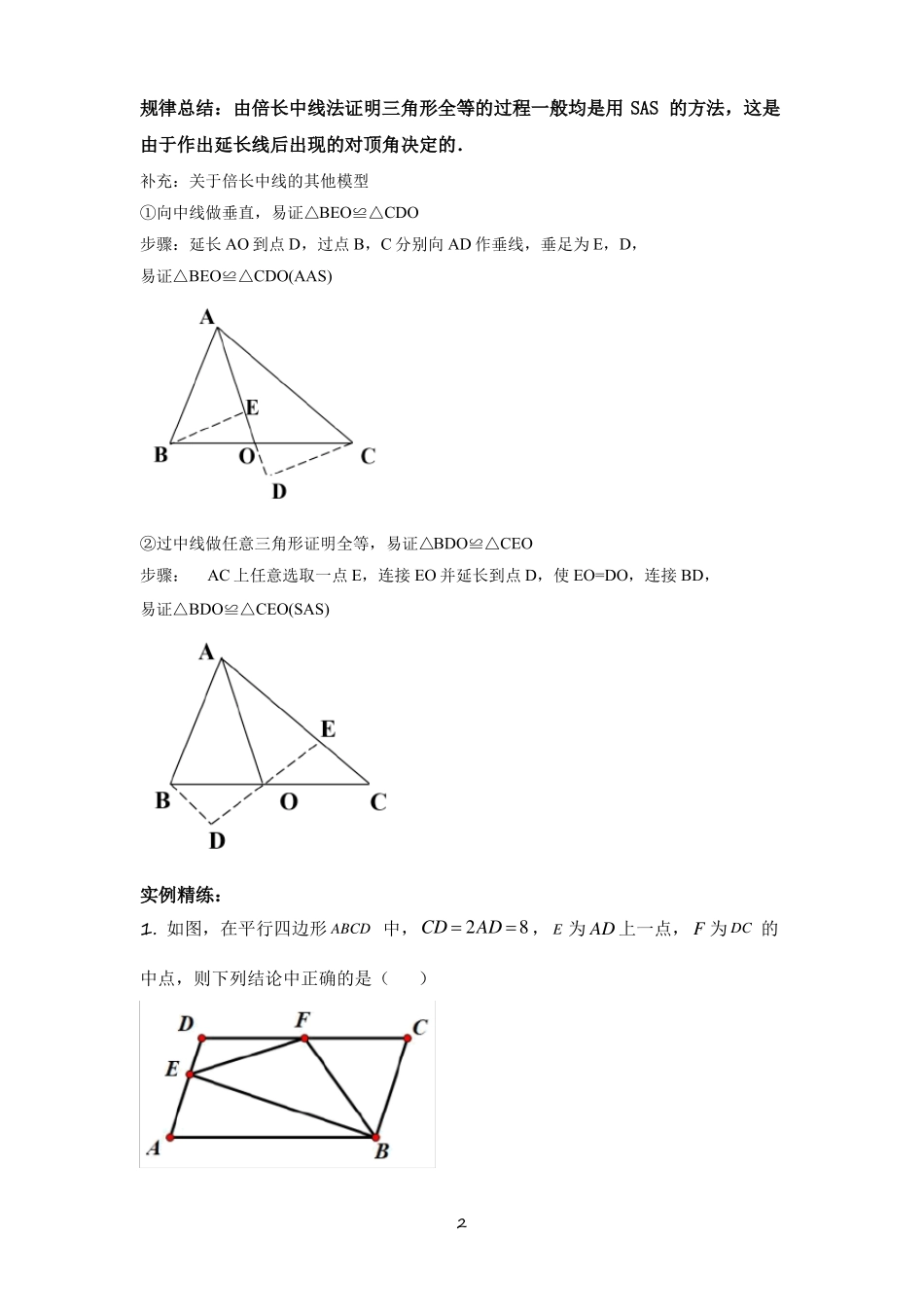
数学模型-倍长中线模型模型分析：倍长中线主要用于证明全等三角形，其主要是在全等三角形的判定过程中，给出中线，通过延长辅助线的方法证明三角形全等及其他，达到解题的目的．其主要的图形特征和证明方法如下图：已知：在三角形ABC中，O为BC边中点，辅助线：延长AO到点D使AO=DO，结论：△AOB≌△DOC证明：延长AO到点D使AO=DO，由中点可知，OB=OC，在△AOB和△DOC中OAODAOBDOCOBOC∴△AOB≌△DOC同理下图中仍能得到△AOB≌△DOC1规律总结：由倍长中线法证明三角形全等的过程一般均是用SAS的方法，这是由于作出延长线后出现的对顶角决定的．补充：关于倍长中线的其他模型①向中线做垂直，易证△BEO≌△CDO步骤：延长AO到点D，过点B，C分别向AD作垂线，垂足为E，D，易证△BEO≌△CDO(AAS)②过中线做任意三角形证明全等，易证△BDO≌△CEO步骤：AC上任意选取一点E，连接EO并延长到点D，使EO=DO，连接BD，易证△BDO≌△CEO(SAS)实例精练：1.如图，在平行四边形ABCD中，CD2AD8，E为AD上一点，F为DC的中点，则下列结论中正确的是（）2A.BF4【答案】D【解析】B.ABC2ABFD.S四边形DEBC2SEFBC.EDBCEB【分析】根据平行四边形的性质可以得到CD2AD2BC8，且F为DC的中点，所以CFBC4,由此可判断A选项；再结合平行线的性质可以得到CFBFBA，由此可判断B选项；同时延长EF和BC交于点P，DFCF,DFEPFC,DFCP可以证得DFECFP，所以EDBCCPBCBP由此可以判断C选项；由于DFECFP，所以S四边形DEBCSBEP，由此可以判断D选项；【详解】四边形ABCD是平行四边形CD2AD2BC8CFBC4由于条件不足，所以无法证明BF4,故A选项错误；CFBC4CFBFBCDC∥ABCFBFBCFBAABC2ABF故B选项错误；同时延长EF和BC交于点PADBPDFCP3DFCF在△DFE和CFP中：DFEPFCDFCPASADFECFPEDBCCPBCBP由于条件不足，并不能证明BPBE，故C选项错误；DFECFPS四边形DEBCSBEPF为DC的中点SBEP2SBEFS四边形DEBC故D选项正确；故选：D.【点睛】本题主要考查平行四边形的性质，以及全等三角形的判定，根据题意作出相应的辅助线是求解本题的关键.2.如图，ABCD，BCD90，AB1,BCCD2,E为AD上的中点，则BE＝______．4【答案】【解析】52【分析】延长BE交CD于点F，证ABE≌DFE，则BE=EF=三角形BCF中运用勾股定理求出BF长即可.【详解】解：延长BE交CD于点F AB平行CD，则∠A=∠EDC，∠ABE=∠DFE，又E为AD上的中点，∴BE=EF,所以ABE≌DFE.∴BEEF∴CF1在直角三角形BCF中，BF=1222=5.∴BE1BF，故再在直角21BF,ABDF1215.BF22【点睛】本题的关键是作辅助线，构造三角形全等，找到线段的关系，然后运用勾股定理求解.53.如图，ABC中，D为BC的中点，E是AD上一点，连接BE并延长交AC于F，BEAC，且BF9，CF6，那么AF的长度为__．3【答案】；2【解析】【分析】延长AD至G使ADDG，连接BG，得出ACDGBD得出ACBGBE，所以得出AEF是等腰三角形，根据已知线段长度建立等量关系计算．【详解】如图：延长AD至G使ADDG，连接BG在ACD和GBD中：CDBDADCBDGADDG∴ACDGBD∴CADG,ACBG BEAC6∴BEBG∴GBEG BEGAEF∴AEFEAF∴EFAF∴AFCFBFEF即AF69EF∴AF32【点睛】倍长中线是常见的辅助线、全等中相关的角的代换是解决本题的关键．4.如图，平行四边形ABCD中，CEAD于E，点F为边AB中点，1ADCD，CEF40，则AFE_________2【答案】30【解析】CB交于点G，【分析】延长EF、连接FC，先依据全等的判定和性质得到FEFG，依据直角三角形斜边上的中线等于斜边的一半，得到FCFEFG，依据平行四边形的对边相等及等量代换得到BFBC，依据三角形等边对等角得到FCGG50、BFCFCG50，依据三角形内角和得到GFC，通过作差即得所求.7【详解】解：延长EF、CB交于点G，连接FC， 平行四边形ABCD中，∴AD//BC，ABCD,ADBC,∴AGBF，AFEBFG，...