课件等腰三角形4课时VIP免费

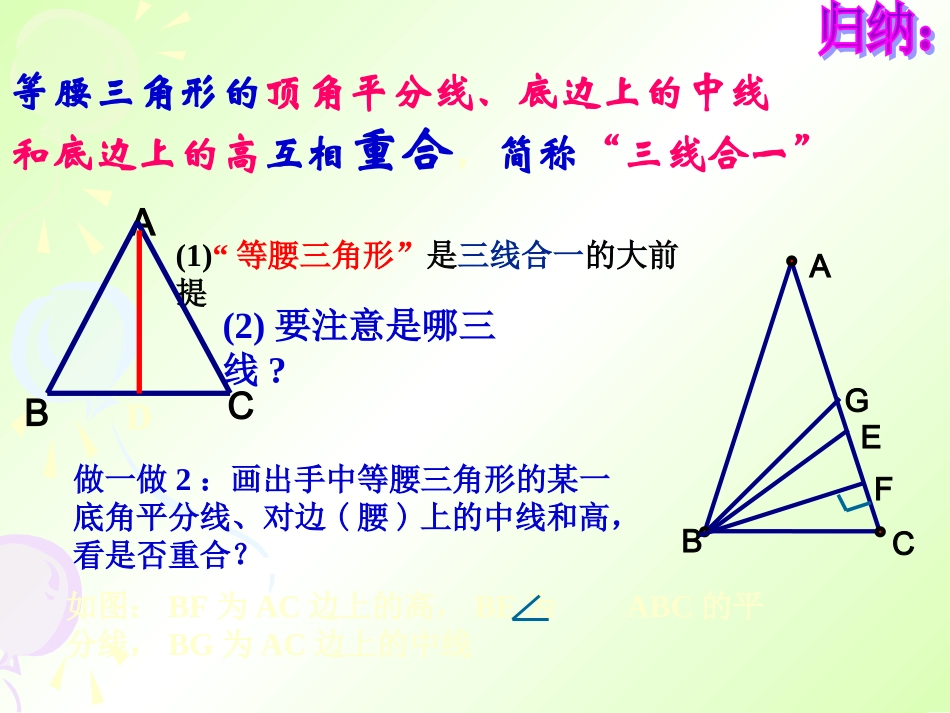
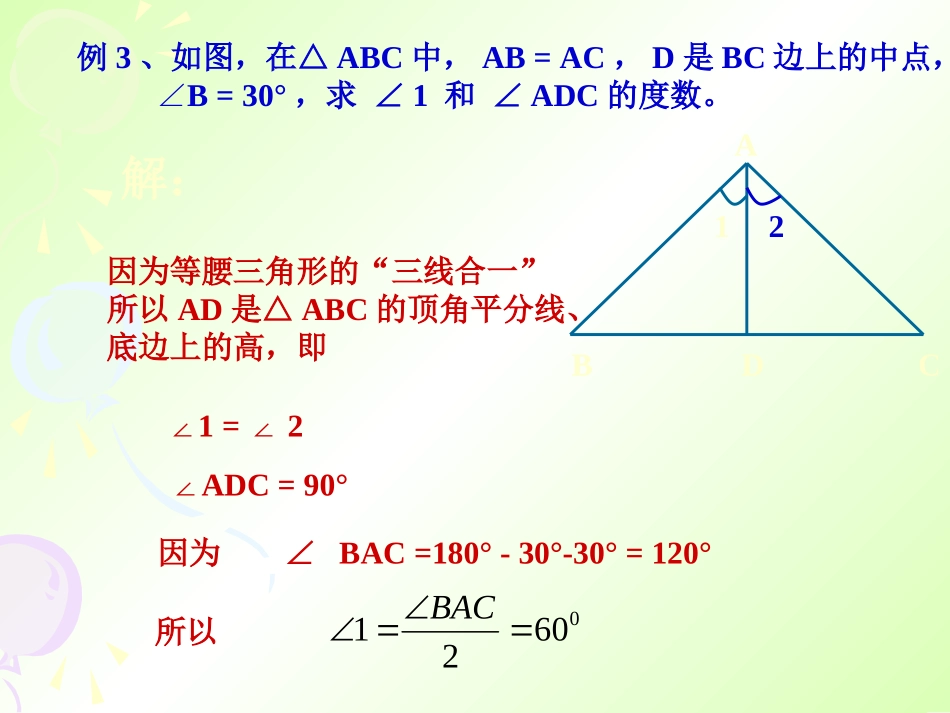
等腰三角形(2)要注意是哪三线?做一做2：画出手中等腰三角形的某一底角平分线、对边(腰)上的中线和高，看是否重合？等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合，简称“三线合一”(1)“等腰三角形”是三线合一的大前提GECBAF如图：BF为AC边上的高，BE为ABC的平分线，BG为AC边上的中线CABD例3、如图，在△ABC中，AB=AC，D是BC边上的中点，∠B=30°，求∠1和∠ADC的度数。ABC12D解：因为等腰三角形的“三线合一”所以AD是△ABC的顶角平分线、底边上的高，即∠1=2∠∠ADC=90°因为∠BAC=180°-30°-30°=120°所以06021BAC1.等腰三角形一个角为70°,它的另外两个角为___________________2.等腰三角形一个角为110°,它的另外两个角为________70°,40°或55°,55°35°,35°巩固练习:3等腰三角形有两边长为6和8，则该等腰三角形的周长为4.等腰三角形有两边长为4和8，则该等腰三角形的周长为20或22201、判断下列命题是否正确。（1）等腰三角形的角平分线、中线和高互相重合。（）（2）有一个角是60°的等腰三角形，其它两个内角也为60°。（）2、如图，在△ABC中，已知AB=AC，AD为∠BAC的平分线，且∠2=25°，求∠ADB和∠B的度数。D12ABC补充例题：DABC的度数；时，求）当（BCDA1402的度数；时，求）当（BCDA3达标练习二(A水平)一、填空题：1、等腰三角形若两边长为3和7，则其周长为________。2、如果等腰三角形的一个底角为50°，那么其余两个角为______和______。3、如果等腰三角形的顶角为80°，那么它的一个底角为________。二、判断题：1、等腰三角形的底角都是锐角()2、钝角三角形不可能是等腰三角形()√×1750°80°50°达标练习二(B水平)1、若等腰三角形的一个内角为40°,则它的另外两个内角为__________________2、若等腰三角形的一个内角为120°,则它的另外两个内角为______70°,70°或40°，100°30°,30°①顶角+2×底角=180°②顶角=180°－2×底角③底角=（180°－顶角）÷2结论:在等腰三角形中，已知一个角，就可以求出另外两个角。④当已知任意一个内角时,则要分情况讨论5.5.已知如图：在已知如图：在△ABC中，AB=AC，点M在△ABC内，且MB=MC。求证：∠ABM=∠ACMAABBCCMM66..已知：如图，在已知：如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，（1）图中有几个等腰三角形？（2）求△ABC各角的度数。AABBCCDD挑战：已知等腰三角形一腰上的中线将三角形周长分成２：１两部分，已知三角形底边长为５，求腰长？解：如图，令CD＝x，则AD＝x，AB＝2x∵底边BC＝5∴BC＋CD＝5＋xAB＋AD＝3x∴(5+x)：3x＝2:1或3x：(5+x)=2:1ＡＢＣＤxx2x5例例4.4.如图，已知△如图，已知△ABCABC中，中，AB=ACAB=AC，，BD=BCBD=BC，，AD=DE=EB,AD=DE=EB,求求∠∠AA的度数的度数..解：设∠A=x，∠EBD=y，∠C=z∵AB=ACABC=C=z∴∠∠∵BD=BCC=BDC=z∴∠∠∵BE=DEEBD=EDB=90°∴∠∠∵AD=DEA=AED=x∴∠∠又∵∠BDC=A+ABD∠∠，∠AED=EBD+EDB∠∠（三角形的外角等于和它不相邻的两个内角的和）∠A+ABC+ACB=180°∠∠（三角形内角和为180°）∴解得x=45°即：∠A=45°1802zzxyxzyxABCDExyzxyz挑战５：如图，已知CE、CF分别平分∠ACB和它的外角，EF∥BC，EF交AC于D，你能说明DE＝DF的理由吗？FDEABCG1、等腰三角形的性质：等边对等角2、等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合（三线合一）3、“三线合一”性质在实际应用中，只要推出其中一个结论成立，其它两个结论一下成立，所以关键是寻找其中一个结论成立的条件。再见！