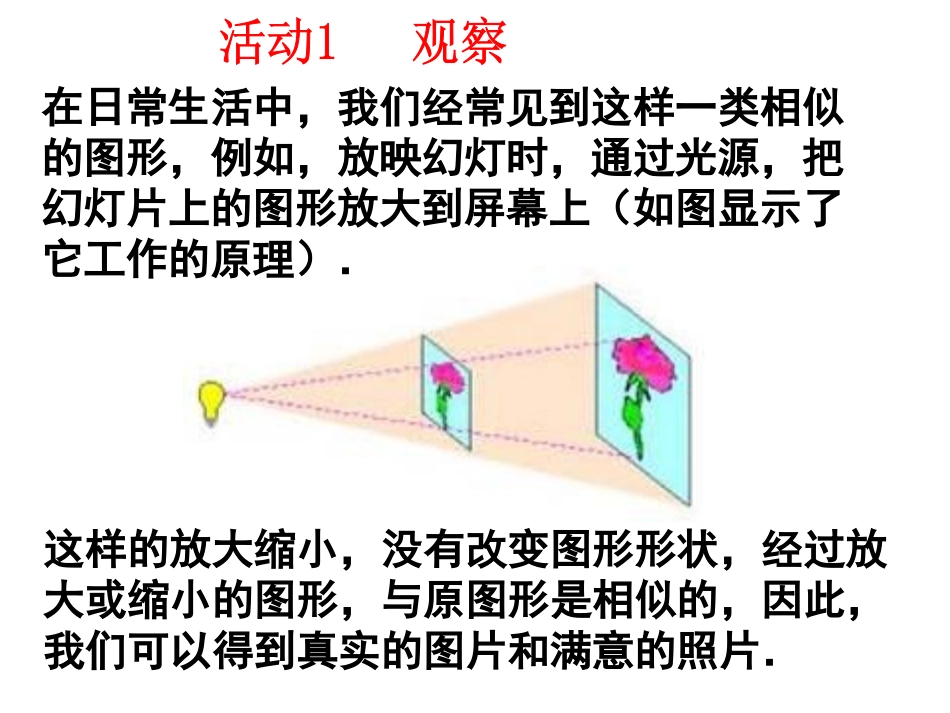
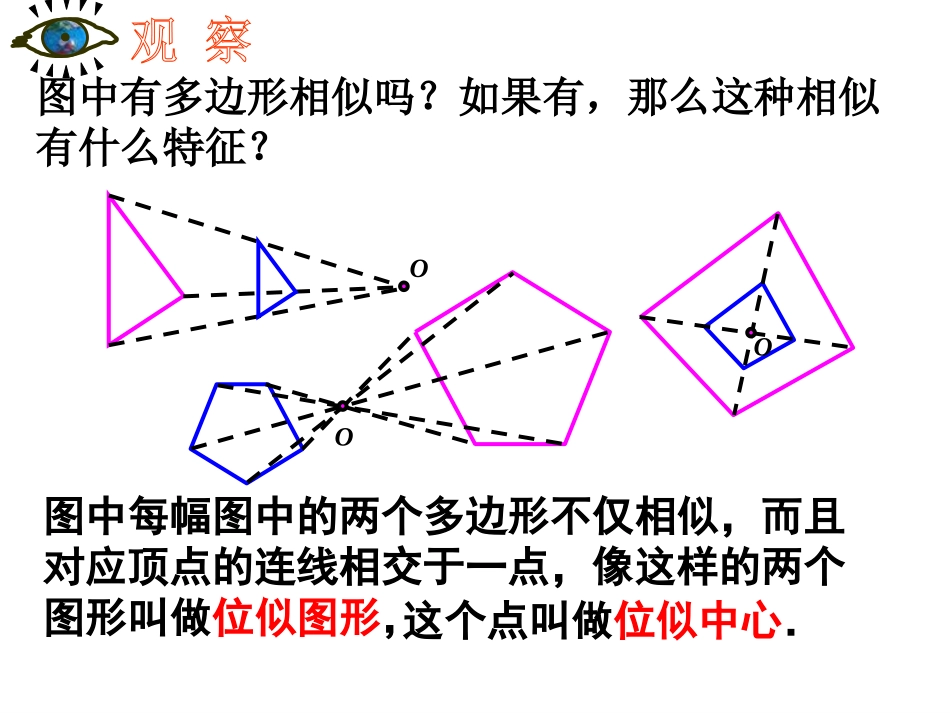
这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片.在日常生活中,我们经常见到这样一类相似的图形,例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理).图中有多边形相似吗?如果有,那么这种相似有什么特征?图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形,OOO这个点叫做位似中心.概念与性质1.位似图形的概念如果两个图形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.相似对应顶点的连线相交一点对应边互相平行(或在同一直线上)明确如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边平行,像这样的两个图形叫位似图形.特征:1、位似图形一定是相似形,反之不一定。2、判断位似图形时要注意首先它们必须是相似形,其次每一对对应点所在直线都经过同一点。这个点叫做位似中心,这时的相似比又叫位似比。1.判断下列各对图形是不是位似图形.(1)正五边形ABCDE与正五边形A′B′C′D′E′;(2)等边三角形ABC与等边三角形A′B′C′.思考:是否相似图形都是位似图形?是是不一定判断下面的正方形是不是位似图形?(1)不是ACDBFEG显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形思考:位似图形有何性质?如果∆OAB和∆OCD是位似图形,那么AB∥CD吗?为什么?解:ABCD.∥理由是:∆OAB和∆OCD是位似图形,∆OAB∆OC∽D∠OAB=∠CABCD.∥ABCDO注意:对应边OB与OD在同一直线上.2.位似图形的性质从第(1),(2)图中,我们可以看到,△OAB∽△OA′B′,则OAOA′=OBOB′=ABA′B′.从第(3)图中同样可以看到AFAD=APAC=AEAB=EPBC=FPDC性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比.概念与性质若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=()。OAA’BCB’C’1:2作出下列位似图形的位似中心:O点O即为所求作出下列位似图形的位似中心O点O即为所求2.分别在线段OA、OB、OC、OD上取点A'、B'、C'、D',使得3.顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.21''''ODODOCOCOBOBOAOAODABCA'B'C'D'利用位似,可以将一个图形放大或缩小.例如,要把四边形ABCD缩小到原来的1/2,1.在四边形外任选一点O(如图),A’B’C’D’即为所求对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A‘,B’、C‘、D’,使得呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.21''''ODODOCOCOBOBOAOAODABCA'B'C'D'ODABC探究A’B’C’D’即为所求2.如图,以O为位似中心,将△ABC放大为原来的两倍.OABC①作射线OA、OB、OC②分别在OA、OB、OC上取点A'、B'、C'使得1'''2OAOBOCOAOBOC③顺次连结A'、B'、C'就是所要求图形A'B'C'△A’B’C’即为所求我们学习了在平面直角坐标系中,如何用坐标表示某些平移、轴对称、旋转(中心对称)等变换,相似也是一种图形的变换,一些特殊的相似(如位似)也可以用图形坐标的变化来表示。yo246-2-4-6246-2-4-6xAA′B′A′A′′′B′B′′′B在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.A′(2,1),B′(2,0)A〞(-2,-1),B〞(-2,0)观察对应点之间的坐标的变化,你有什么发现?yo246-2-4-6246-2-4-6x-10-88-121012A′B′B′′′B′A′A′′′C′′C′在平面直角坐标系中,△ABC三个顶点的坐标分别为A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2画它的位似图形.放大后对应点的坐标分别是多少?A′(4,6),B′(4,2),C′(12,4)还有其他办法吗?CBA观察对应点之间的坐标的变化,你有什么发现?在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k例如:点A(x,y)的对应点为...