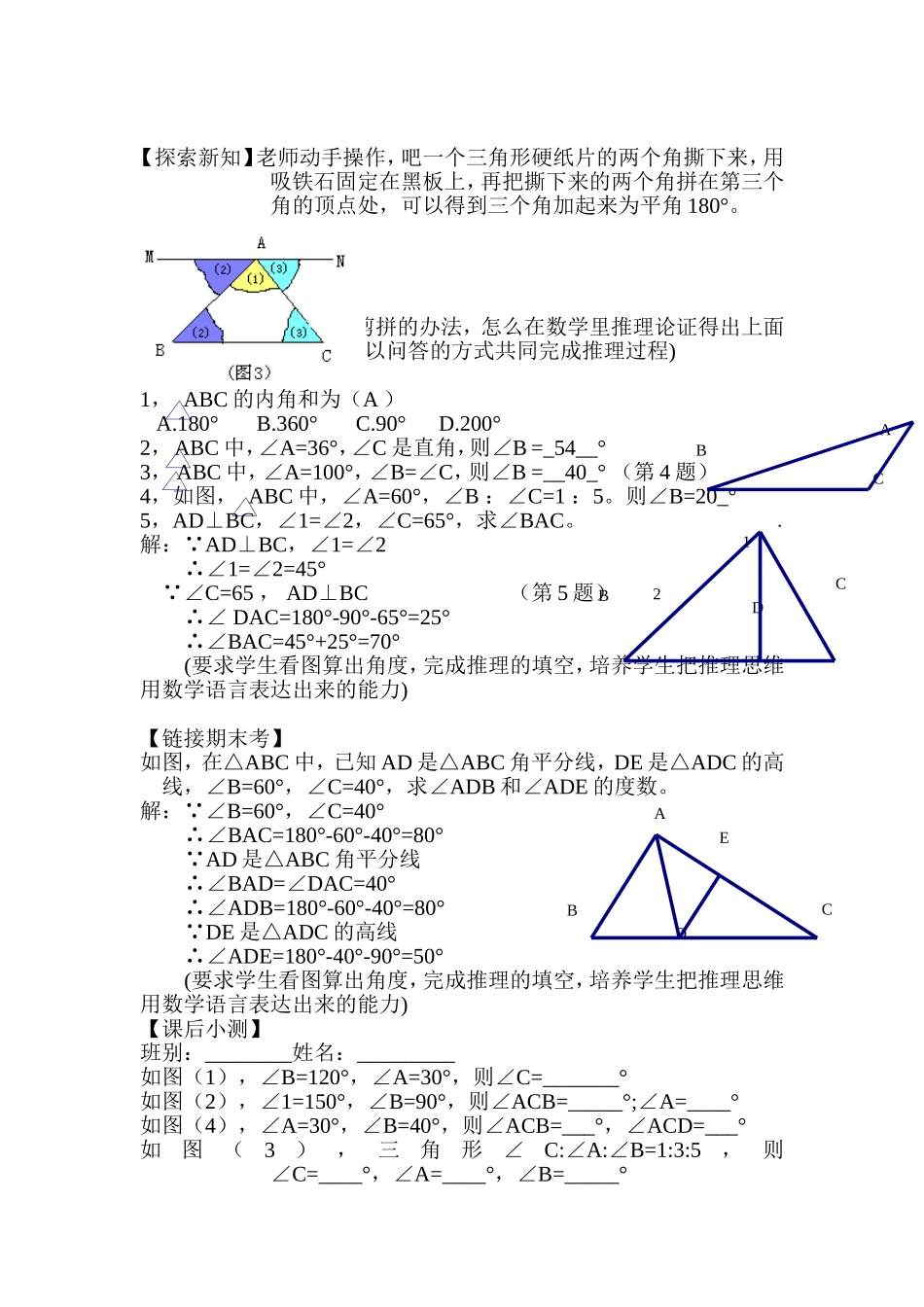
80°60°1240°50°90°240°30°12160°DBAC1AB∥CD27.2.1三角形内角和石榴林初一数学备课组●教材分析及教材处理本节课是与三角形有关的角的第一节课,计划一节课完成。这节课是下几节课《三角形外角》以及《多边形的内角》的基础,对后续学习的影响很大。为了体现延续性,本节课不但要知道内角和是180°,还要注重培养学生看图算角,图上作业的能力,以及训练简单的推理思维。●教学模式与学习方式设计★学情分析小学阶段,学生已经了解过关于三角形的只是,基本上都是到三角形的三个内角之和为180°,但是但是还不知道为什么三角形的内角和是180°,知其然而不知其所以依然。让学生明白为什么三角形内角和为180°,这是我们这节课要学习的。在小学阶段,关于三角形内角和的看图练习学生做过,但是小学阶段的图形变化不多,在这节课还要增加图形的变化,提高学生的看图推理能力。★三维教学目标【知识与能力】:掌握三角形内角和定理,能应用三角形内角和定理看图解决问题,会进行简单的推理【过程与方法】:经历实验活动的过程,得出三角形的内角和定理,并体验用平行线的性质推出这一定理的过程【情感态度与价值观】:让学生展示学生学会的知识,产生成功的愉悦体验,产生学习的兴趣,让学生愿意去学。★教学重点:三角形内角和定理★教学难点:三角形内角和定理的推理过程★教具准备:三角形硬纸片,小吸铁石★本节课的设计思路:通过课前自测题,做四个简单的三角形内角和的看图算角题目,既然学生已经会做这样的关于三角形内角和的简单题目,就让学做,让学生产生成功的体验,产生学习兴趣。也是对小学学的只是的一个复习,然后通过老师的一个提问,引入到为什么三角形内角和为180°,而不是200°或者150°,激发学生的求知欲望。然后通过直观的教具,让学生观察,帮助学生理解三角形内角和定理的推理过程,突破本节课的教学难点。然后还好回到本节课的重点,运用三角内角和和定理看图算角,让学生当堂练习以设计好的有难度梯度的练习题,然后老师讲评。最后再设计一个链接期末训练题,给优生更大的空间。★教学过程【课前自测】CBAA21CBDABCDE【探索新知】老师动手操作,吧一个三角形硬纸片的两个角撕下来,用吸铁石固定在黑板上,再把撕下来的两个角拼在第三个角的顶点处,可以得到三个角加起来为平角180°。想一想,如果我们不用剪拼的办法,怎么在数学里推理论证得出上面的结论呢?(师生互动,以问答的方式共同完成推理过程)【课堂训练】1,ABC的内角和为(A)A.180°B.360°C.90°D.200°2,ABC中,∠A=36°,∠C是直角,则∠B=_54__°3,ABC中,∠A=100°,∠B=∠C,则∠B=__40_°(第4题)4,如图,ABC中,∠A=60°,∠B:∠C=1:5。则∠B=20_°5,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC。解: AD⊥BC,∠1=∠2∴∠1=∠2=45° ∠C=65,AD⊥BC(第5题)∴∠DAC=180°-90°-65°=25°∴∠BAC=45°+25°=70°(要求学生看图算出角度,完成推理的填空,培养学生把推理思维用数学语言表达出来的能力)【链接期末考】如图,在△ABC中,已知AD是△ABC角平分线,DE是△ADC的高线,∠B=60°,∠C=40°,求∠ADB和∠ADE的度数。解: ∠B=60°,∠C=40°∴∠BAC=180°-60°-40°=80° AD是△ABC角平分线∴∠BAD=∠DAC=40°∴∠ADB=180°-60°-40°=80° DE是△ADC的高线∴∠ADE=180°-40°-90°=50°(要求学生看图算出角度,完成推理的填空,培养学生把推理思维用数学语言表达出来的能力)【课后小测】班别:________姓名:_________如图(1),∠B=120°,∠A=30°,则∠C=_______°如图(2),∠1=150°,∠B=90°,则∠ACB=_____°;∠A=____°如图(4),∠A=30°,∠B=40°,则∠ACB=___°,∠ACD=___°如图(3),三角形∠C:∠A:∠B=1:3:5,则∠C=____°,∠A=____°,∠B=_____°(1)(2)(3)(4)★板书设计课前小测★教学反思纵向与上届相比,以前由于对教材理解不够透,对学情认识不够清,有太多的时间与三角形内角和定理的概念和推理过程,然而学生其实都已经知道三角形内角和定理的概念而忽视了内角和的看图算角的应用。而本学期调整了本节课的重心,更注重看图算角的能...