反比例函数几何意义VIP免费

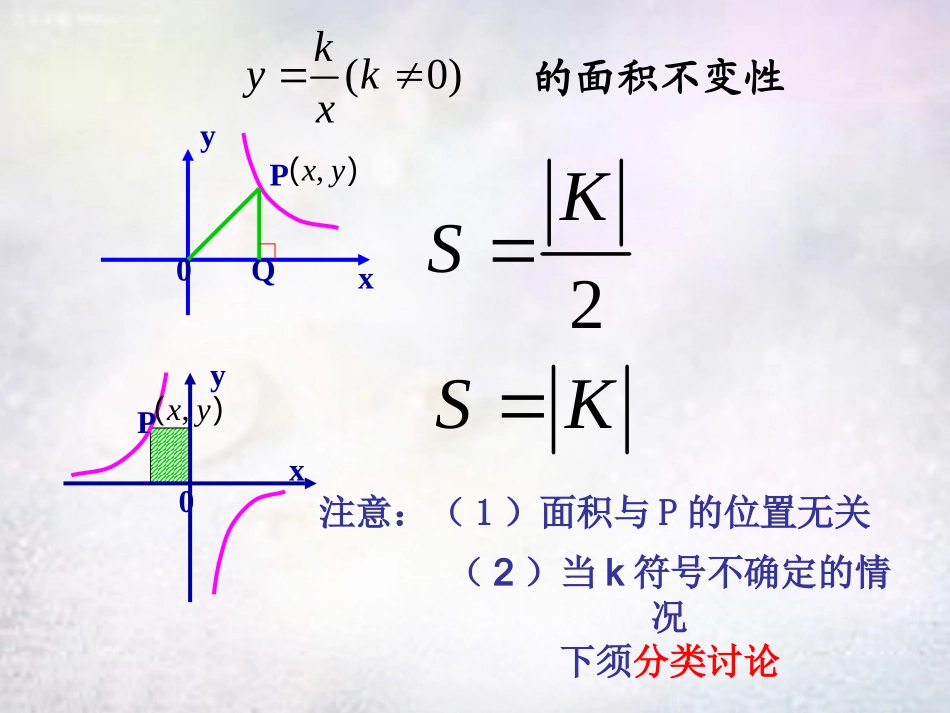
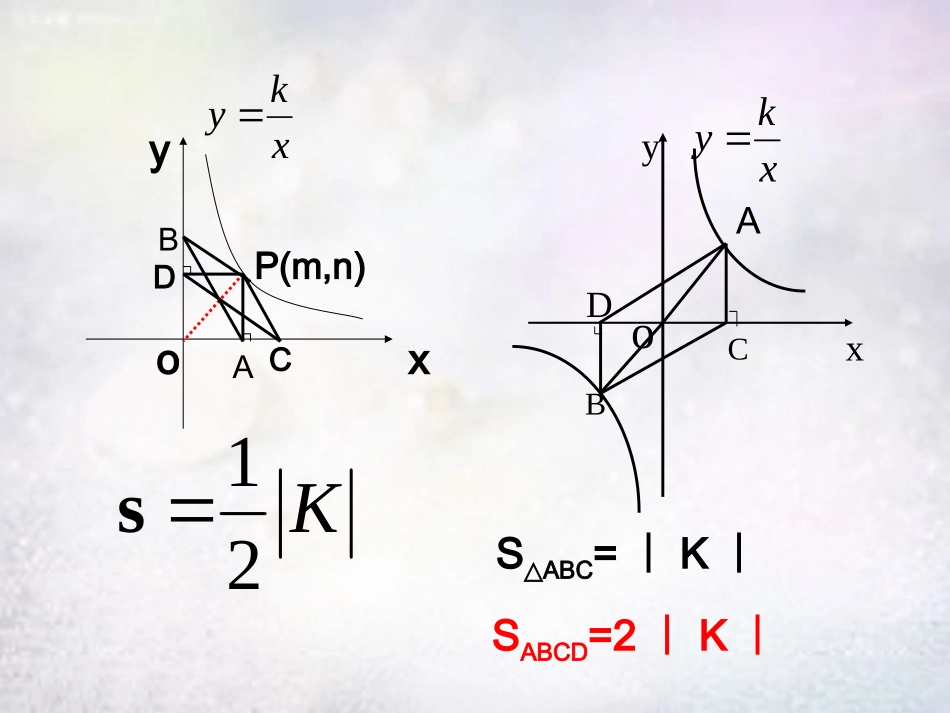
反比例函数K的几何意义2KSSK的面积不变性(0)kykx注意：（1）面积与P的位置无关（2）当k符号不确定的情况下须分类讨论PQ0xy）（yx,P0xy）（yx,SABC△=︱K︱SABCD=2︱K︱BDoyP(m,n)xkyxABCDCoxxkyyAK21sksPBCkSSSkSSCOPOCPCBOPBOPBCCBOPBO21两点关于原点对称，、PBy⊥轴于点B,直线PC经过原点。P(m,n)AoyxP/kSAPP2KmnAPPAPmnAPnmnmPAPSAPp22221212,2.,,,////则解：设1．如图，反比例函数y＝kx(k≠0)的图象上有一点A，AB平行于x轴交y轴于点B，△ABO的面积是1，则反比例函数的解析式是()A．y＝12xB．y＝1xC．y＝2xD．y＝14xC练习2．如图，P(x，y)是反比例函数y＝3x的图象在第一象限分支上的一个动点，PA⊥x轴于点A，PB⊥y轴于点B，随着自变量x的增大，矩形OAPB的面积()A．不变B．增大C．减小D．无法确定A变式：如图，在直角坐标系中，点A是x轴正半轴上的一个定点，点B是双曲线上的一个动点，当点B的横坐标逐渐增大时，的面积将会（）•A．逐渐增大•B．不变•C．逐渐减小•D．先增大后减小3yx0x（）OAB△xyOABC3．双曲线y＝4x与y＝2x在第一象限内的图象如图所示，作一条平行于y轴的直线分别交双曲线于A，B两点，连接OA，OB，则△AOB的面积为()A．1B．2C．3D．4A4．如图，函数y＝－x与函数y＝－4x的图象相交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，D，则四边形ACBD的面积为()A．2B．4C．6D．8D5．如图，A是反比例函数图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，△ABP的面积为2，则这个反比例函数的解析式为_________．y＝4x6．已知反比例函数y＝6x在第一象限的图象如图所示，点A在其图象上，点B为x轴正半轴上一点，连接AO，AB，且AO＝AB，则S△AOB＝____．67．如图，在反比例函数y＝－4x(x＞0)的图象上有三点P1，P2，P3，它们的横坐标依次为1，2，3，分别过这三个点作x轴、y轴的垂线，设图中阴影部分的面积依次为S1，S2，S3，则S1＋S2＋S3＝____．4FABCOE图48.如图4，矩形OABC的两边在坐标轴上，且与反比例函数xyxky2OFBES四边形的图像交于点E、F，其中点E、，则k的值．F分别是BC、AB的中点，若四边形OFBE的面积的面积。两点的坐标；，求两点。，图像交于的与一次函数反比例函数已知如图AOBBABAxyxy)2()1(28,提升运用☞☞例1AyOBxMNCD.)2(;)1(的面积求式求这个一次函数的解析POQyxoPQ随堂巩固☞☞12,4,,6.yxykxPQP练习：1、如图已知反比例函数的图象与一次函数的图象相交于两点并且点的纵坐标是MN练习2、如图，已知反比例函数与矩形ABCO交于点M，N，连接OM，ON，M(3，2)，S四边形OMBN＝6，求反比例函数的解析式及B点，N点的坐标．解：设反比例函数的解析式为y＝kx，把M(3，2)代入y＝kx，得k＝6，∴反比例函数的解析式为y＝6x，∴S△OMA＝S△ONC＝3.∵S四边形OMBN＝6，∴S矩形OABC＝6＋3＋3＝12.∵OA＝3，∴AB＝4，∴B(3，4)．∵OC·CN＝6，∴CN＝32，∴N32，4.xBAoy练习3、如图，已知，A,B是双曲线上的两点，)0(kxky（2）在(1)的条件下，若点B的横坐标为3，连接OA,OB,AB，求△OAB的面积。（1）若A(2,3)，求K的值yBAxo（3）若A,B两点的横坐标分别为a,2a，线段AB的延长线交X轴于点C,若求K的值C6AOCS