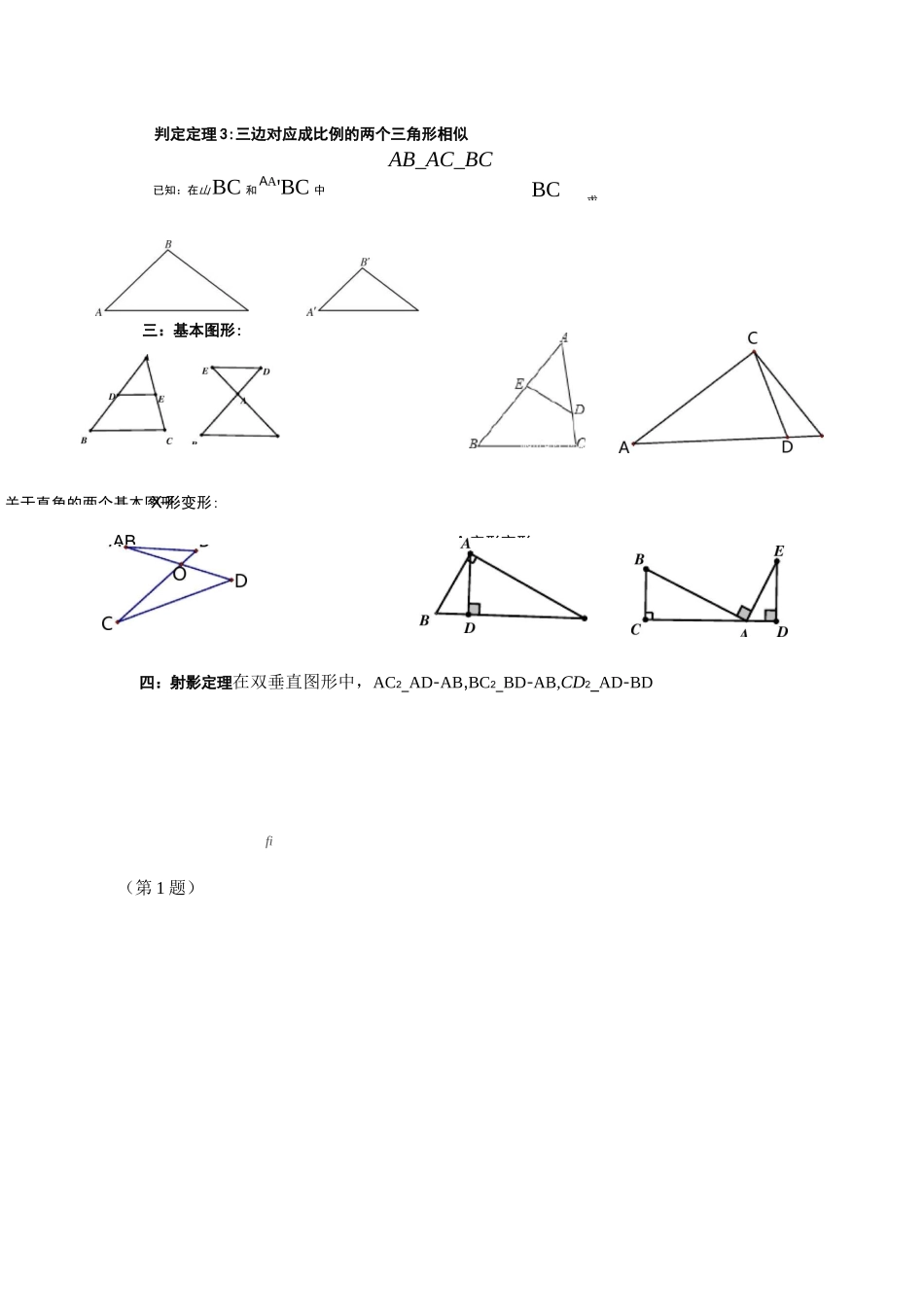
AABCAA,B,C,AB=AC已知在和中,忑药疋ZA=ZA,求证MB—AA,B,C相似三角形的判定定理一:复习1.预备定理:平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似。2.___________________________________________________________前面判定两三角形相似的方法是:.能否简化一下呢?3.____________________________全等三角形的判定方法有:,,,,.4.你猜测下哪些方法可以判定两三角形相似了呢?二:探究新知判定定理1:两角分别对应相等的两个三角形相似已知:在AABC和AA,C中,山=ZA,,ZB=ZB,,求证:AABC〜AA,BC,(参看课本68页证明过程)图24.3.3判定定理2:两边对应成比例且夹角相等的两个三角形相似B已知:在山BC和AA'BC中AB_AC_BCBC,求三:基本图形:典型图形:A字形变形:X形变形:AB关于直角的两个基本图形:判定定理3:三边对应成比例的两个三角形相似四:射影定理在双垂直图形中,AC2_AD-AB,BC2_BD-AB,CD2_AD-BDfi(第1题)五:AA判相似练习1•如图所示,在△ABC中,AD是zBAC的平分线,AD的垂直平分线EF交BC的延长线于F,交AD于E,求证:AABF〜ACAF2•如图,△ABC.△DEF均为等边三角形,D、E分别在AB、BC上,请找出一个与△DBE相似的三角形,并给予证明。3•在3BC中,AB=AC,点P、D分别是BC、AC边上的点,且zAPD=zB.(1)求证:AC・CD二CP・BP;(2)若AB=10,BC=12,当PDllAB时,求BP的长4•如图,在3BC中,zBAC=90。,BC的垂直平分线交BC于点E,交CA的延长线于D,交AB于点F,求证:AE2二EF・ED.六:SAS判相似5.已知:如下图所示,在正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点.AADQ与AQCP是否相似?为什么?6•如图,D为MBC的边AB上—点,若AB=12,AC=15,AD=8,在AC边上取-点E,使△ADE与3BC相似,求AE的长.7•如图所示,在△ABC中,zC二90°,AC二6cm,BC二8cm,点P从点B出发沿边BC向点C以2cm/s的速度移动点Q从C点出发沿CA边向点A以1cm/s的速度移动•如果P、Q同时出发,几秒钟后,可使△PCQ与MBA相似?8•直线y二ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=£(x>0)x相交于点p,PC±x轴于点C,且PC=2,点A的坐标为m•(1)求双曲线的解析式;(2)若点Q为双曲线上点P右侧的一点,且QH丄x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.9•如图,在直角三角形POQ中上POQ=90°QP=2OQ点P在反比例函数y二4x上,点Q在反比例函数y二k上,求K的指.X中3BC相似的是(滋C.△ADE"AEF10.如图,在直角梯形ABCD中,ADllBC,zABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若/AD与2BC是相似三角形,求AP的长度.11.节节高69页11题.七:SSS判定相似12•如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与左图如图,在矩形ABCD中,E,F分别是CD,BC上的点,若zAEF=90°,则一定有()在RfABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式是()A.b=a+cB.b=acC.b2=a2+c2D.b=2a=2c16.在厶ABC中,AB=AC,zA=36°,BD平分zABC交AC于点D,若AC=2,贝9AD的长A.△ADE"ECFB.AECF-AAEFD.AAEF^AABF