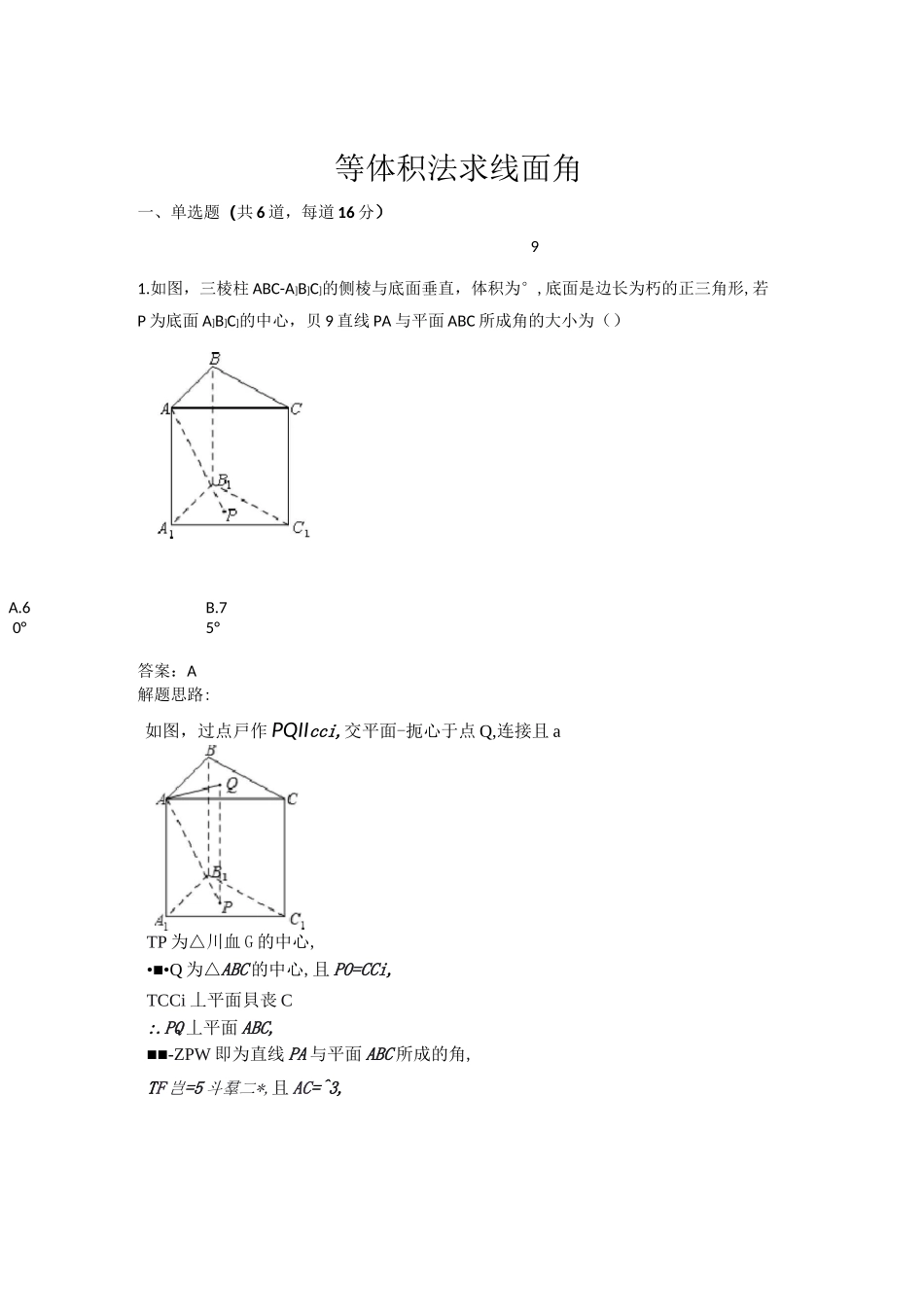
A.60°B.75°等体积法求线面角一、单选题(共6道,每道16分)91.如图,三棱柱ABC-A]B]C]的侧棱与底面垂直,体积为°,底面是边长为朽的正三角形,若P为底面A]B]C]的中心,贝9直线PA与平面ABC所成角的大小为()答案:A解题思路:如图,过点戸作PQIIcci,交平面-扼心于点Q,连接且aTP为△川血G的中心,•■•Q为△ABC的中心,且PO=CCi,TCCi丄平面貝丧C:.PQ丄平面ABC,■■-ZPW即为直线PA与平面ABC所成的角,TF岂=5斗羣二*,且AC=^3,在AABC中,Q为中心,AO=-x^-x^=l,_32ft中,PQ二靠,貝Q=l,「•tatiZ王炉7L.'.Z^O=60Q.故选A.试题难度:三颗星知识点:直线与平面所成的角2.如图,在正四棱锥P-ABCD中,已知PA=AB=J^,若M为PA的中点,则直线BM与平面34A3B$2^2若C.I答案:C解题思路:求出点B到平面PAD的距鬲然后构建直角三角形求解.如图,连接EDAC,设BD,AC的交点为6连接F6AS利用等体积法%.通=耳寸皿求岀点用到平面PQ的距离,由题意得,hPAD为等边三角形,PAD所成角的正弦值是()C2在正方形■麻CD中,AB=J1,易得OA=l,在Hr△月OP中,OA=lfE4血,:.OP=lf设点B到平面PAD的距离为氏■■T7一卩■AFPJSD_FE-FAD,.•丄乂1乂1=2父日乂晅,解得已=项,3323在等边三角形芒毎中,取为羽的中点,二召胚L肚.5停鱼曲二昼,22设直线瓦直与平面卫3所成的角为出贝1]如&二旦二二卫1,聪逅3即直线占站与平面左妙所成角的正弦值是—.3故选C.试题难度:三颗星知识点:直线与平面所成的角3.如图,在三棱锥卩一抠。中,已知知丄平面他C,FA",PAEC仝,则UP与平面抽月所成角的正弦值是()A.B.孑C.D.答案:C解题思路:如图,过点C作CD丄平面丹丑于点D连接PD,3T丹丄平面.4BC,刊1=3,PB=PC=BC=^,:.^=AC=^j3,△昭方匚杲底边为侑的等腰三角形,■■-△曲C底边上的高为击尸—乎=3忑,.'.笙肿亡二寸®忑,解得3=还■・■°尸与平面尸期所戚角的正弦值为££=迹=遁・PC63-故选C.试题难度:三颗星知识点:直线与平面所成的角4.如图,在三棱锥S-ABC中,底面ABC是边长为2的等边三角形,SA丄底面ABC,SA=3,则直线AB与平面SBC所成角的正弦值为()C^D.l答案:D解题思路:如图,过点川作肿丄平面佃c于点码连接厮;■-■A.4BC是边长为?的等边三角形,£4丄底面一疝cSA=3,:.SB=SC=Ji3,△霸(?是底边长为2的等腰三角形,■■■△朋匚中底边上的高为J(r/W_F"翻,艮卩Ix^x23x3=-x-^2xi75x^-3432:.AF=-f27在RtAABF中,3F=—,且民乙22--sin==—=—?AB24即直线AB与平面SBC-所成角的正弦值为-.4故选D・试题难度:三颗星知识点:直线与平面所成的角5.如图,已知PA=PB=PC,且PA,PB,PC两两垂直,则PA与平面ABC所成角的正弦值为(CF1翻A3B.C.I答案:C解题思路:如图,过点戸作加丄平面川EC于点从连接」仍,则8D即为刮与平面XRC所成的角,设PA=PB=PC=a,••0,PBrFC■两两垂直,■■-△佃c■是边长为血盘的等边三角形,'■'乜二冬按麻-FNC,即)-2\皿-FD=电-仏皿-P盘,一T故选c.试题难度:三颗星知识点:直线与平面所成的角6.如图,已知P是正四面体ABCD的棱AC的中点,则直线PD与平面BCD所成角的正弦值为()A_B."2^21C.D3答案:A解题思路:3如图,过点T作AE1平面眈D于点E,过点尸作珂丄平面占CQ于点尺连接CE,BP,DF,则乙PDF即为直线PD与平面BCD所感的角,易得AE=1PF,设正四面体ABCD的边长为g则其体积为,12丁三棱锥P-BCD的高是四面体高的一半,•••三棱锥尸-月CD的体积为2+•••△边的面积为芈冰冬淖沁=沁如吧4-3在△卫C®中,P^AC中点,农sinAPDF=——二—PD品应故选A.试题难度:三颗星知识点:直线与平面所成的角