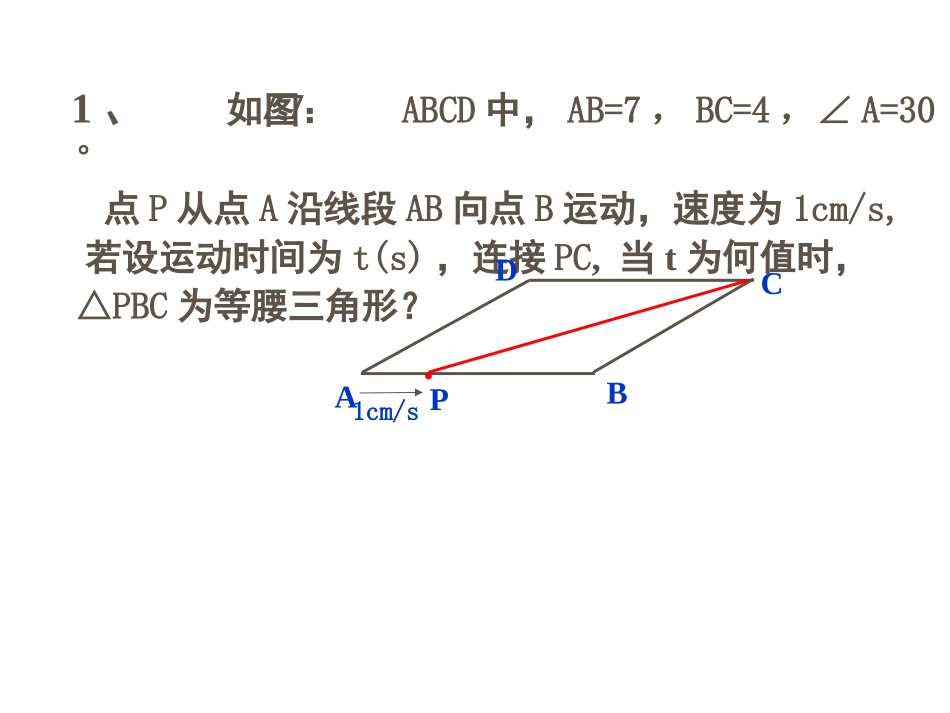
1、掌握动态问题的基本解题方法,提升解题能力。2、培养合作意识,学会合作学习。1、如图:ABCD中,AB=7,BC=4,∠A=30°点P从点A沿线段AB向点B运动,速度为1cm/s,若设运动时间为t(s),连接PC,当t为何值时,△PBC为等腰三角形?DBC1cm/sPA●2、已知:平行四边形ABCD中,AB⊥AC,对角线AC、BD交于0点,将直线AC绕点0顺时针旋转,分别交BC、AD于点E、F。请问:当旋转角为多少度时,四边形ABEF是平行四边形,为什么?3、Rt△PMN中,∠P=90°,PM=PN,MN=8cm,矩形ABCD的长和宽分别为8cm和2cm,C点和M点重合,BC和MN在一条直线上。如果Rt△PMN不动,矩形ABCD沿MN所在直线向右以每秒1cm的速度移动,直到C点与N点重合为止。设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,求y与x之间的函数关系式?ABCDMNP828ABCDMNP828ABCD28解:(1)当0≤x≤2时,∵MC=x,∠PMN=450∴CE=x,GFE∴y=x2(0≤x≤2)21ABCDMNP828ABCDGFHT解:(2)当2<x≤6时,∵MC=x,MF=GF=2,∴CF=GD=x-2∴y重叠=S梯形MCDG=(x-2+x)2=2x-221∴y=2x-2(2<x≤6)ABCDMNP8ABCDGFHT解:(3)当6<x≤8时,∴y=S五边形GMCQH=S梯形GMNH-SΔQCNQ21=12-(8-x)24、如图,在梯形ABCD中,AD∥BC,∠A=∠D,点E是线段AD上的一动点(不与A、D重合),G、F、H分别是BE、BC、CE的中点。(1)试探索四边形ECFH的形状,并说明理由。(2)当点E运动到什么位置时,四边形ECFH是菱形?并加以证明。(3)若(2)中的菱形是正方形,请探索线段EF与线段BC的关系,并证明你的结论。