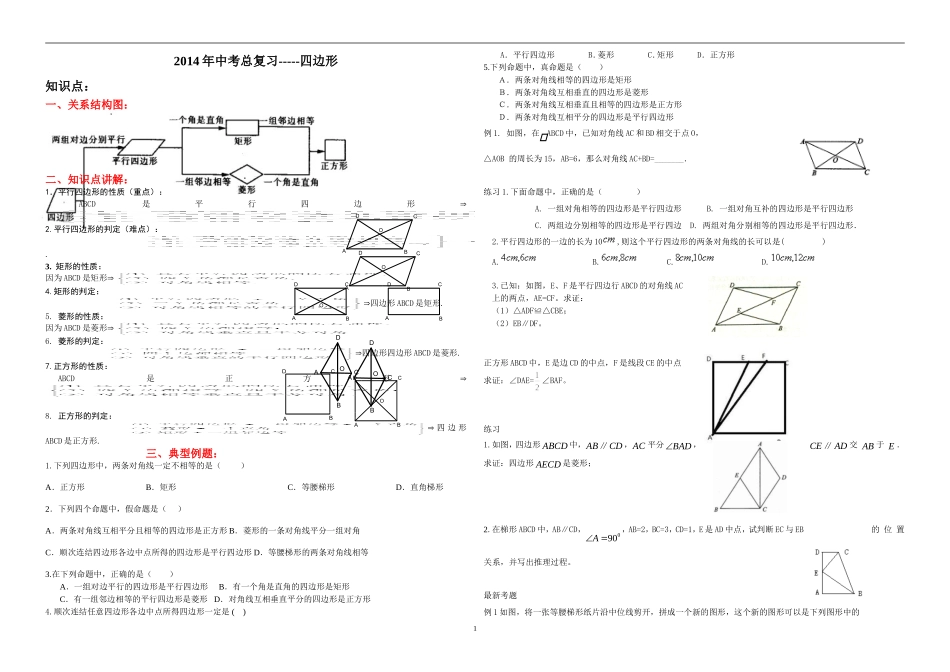
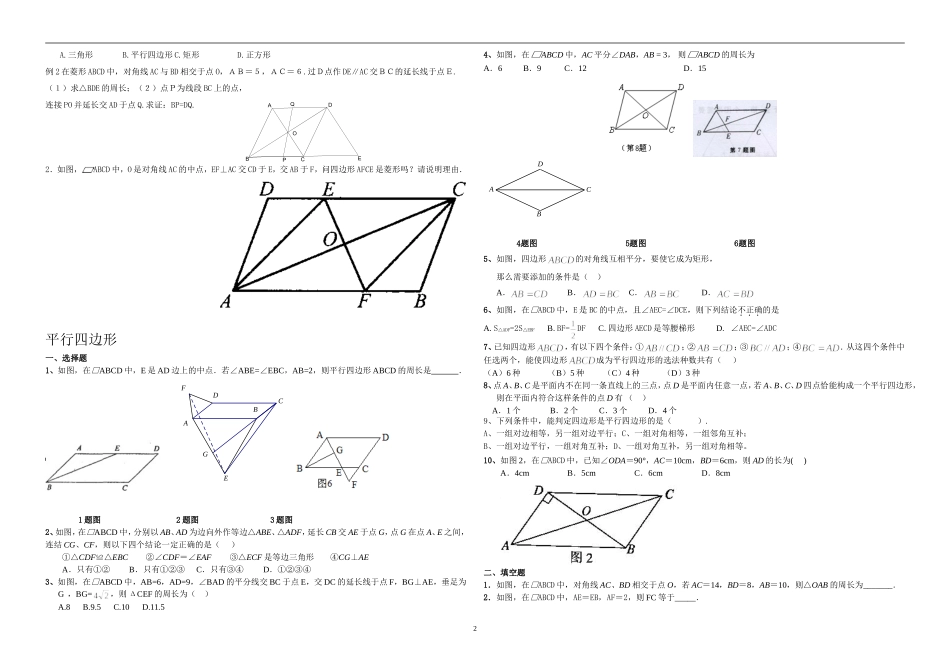
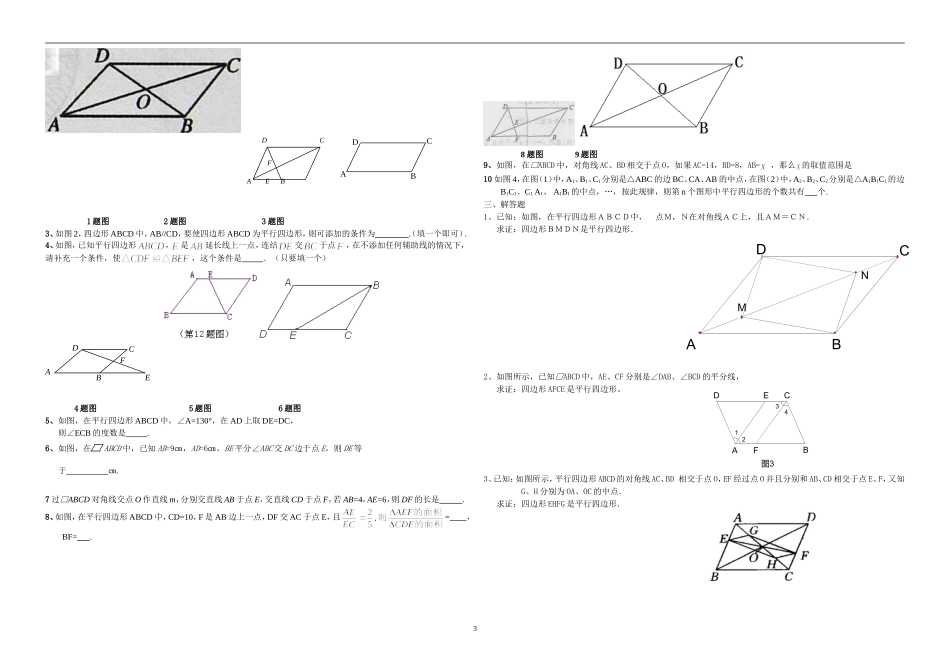
CDABABCDO2014年中考总复习-----四边形知识点:一、关系结构图:二、知识点讲解:1.平行四边形的性质(重点):ABCD是平行四边形2.平行四边形的判定(难点):.3.矩形的性质:因为ABCD是矩形4.矩形的判定:四边形ABCD是矩形.5.菱形的性质:因为ABCD是菱形6.菱形的判定:四边形四边形ABCD是菱形.7.正方形的性质:ABCD是正方形8.正方形的判定:四边形ABCD是正方形.三、典型例题:1.下列四边形中,两条对角线一定不相等的是()A.正方形B.矩形C.等腰梯形D.直角梯形2.下列四个命题中,假命题是()A.两条对角线互相平分且相等的四边形是正方形B.菱形的一条对角线平分一组对角C.顺次连结四边形各边中点所得的四边形是平行四边形D.等腰梯形的两条对角线相等3.在下列命题中,正确的是()A.一组对边平行的四边形是平行四边形B.有一个角是直角的四边形是矩形C.有一组邻边相等的平行四边形是菱形D.对角线互相垂直平分的四边形是正方形4.顺次连结任意四边形各边中点所得四边形一定是()A.平行四边形B.菱形C.矩形D.正方形5.下列命题中,真命题是()A.两条对角线相等的四边形是矩形B.两条对角线互相垂直的四边形是菱形C.两条对角线互相垂直且相等的四边形是正方形D.两条对角线互相平分的四边形是平行四边形例1.如图,在ABCD中,已知对角线AC和BD相交于点O,△AOB的周长为15,AB=6,那么对角线AC+BD=_______.练习1.下面命题中,正确的是()A.一组对角相等的四边形是平行四边形B.一组对角互补的四边形是平行四边形C.两组边分别相等的四边形是平行四边D.两组对角分别相等的四边形是平行四边形.2.平行四边形的一边的长为10,则这个平行四边形的两条对角线的长可以是()A.B.C.D.3.已知:如图,E、F是平行四边行ABCD的对角线AC上的两点,AE=CF。求证:(1)△ADF≌△CBE;(2)EB∥DF。正方形ABCD中,E是边CD的中点,F是线段CE的中点求证:∠DAE=∠BAF。练习1.如图,四边形ABCD中,ABCD∥,AC平分BAD,CEAD∥交AB于E.求证:四边形AECD是菱形;2.在梯形ABCD中,AB∥CD,090A,AB=2,BC=3,CD=1,E是AD中点,试判断EC与EB的位置关系,并写出推理过程。最新考题例1如图,将一张等腰梯形纸片沿中位线剪开,拼成一个新的图形,这个新的图形可以是下列图形中的1ABDOCABDOCADBCADBCOCDBAOCDBAOQPOEDCBAA.三角形B.平行四边形C.矩形D.正方形例2在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6.过D点作DE∥AC交BC的延长线于点E.(1)求△BDE的周长;(2)点P为线段BC上的点,连接PO并延长交AD于点Q.求证:BP=DQ.2.如图,ABCD中,O是对角线AC的中点,EF⊥AC交CD于E,交AB于F,问四边形AFCE是菱形吗?请说明理由.平行四边形一、选择题1、如图,在□ABCD中,E是AD边上的中点.若∠ABE=∠EBC,AB=2,则平行四边形ABCD的周长是.GFEDCBA1题图2题图3题图2、如图,在□ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连结CG、CF,则以下四个结论一定正确的是()①△CDF≌△EBC②∠CDF=∠EAF③△ECF是等边三角形④CG⊥AEA.只有①②B.只有①②③C.只有③④D.①②③④3、如图,在□ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=,则ΔCEF的周长为()A.8B.9.5C.10D.11.54、如图,在□ABCD中,AC平分∠DAB,AB=3,则□ABCD的周长为A.6B.9C.12D.154题图5题图6题图5、如图,四边形的对角线互相平分,要使它成为矩形,那么需要添加的条件是()A.B.C.D.6、如图,在□ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是A.S△ADF=2S△EBFB.BF=DFC.四边形AECD是等腰梯形D.∠AEC=∠ADC7、已知四边形,有以下四个条件:①;②;③;④.从这四个条件中任选两个,能使四边形成为平行四边形的选法种数共有()(A)6种(B)5种(C)4种(D)3种8、点A、B、C是平面内不在同一条直线上的三点,点D是平面内任意一点,若A、B、C、D四点恰能构成一个平行四边形,则在平面内符合这样条件的点D有()A.1个B.2个C.3个D.4个9、下列条件中,能判定四边形是平行四...