函数的单调性 (2)VIP免费

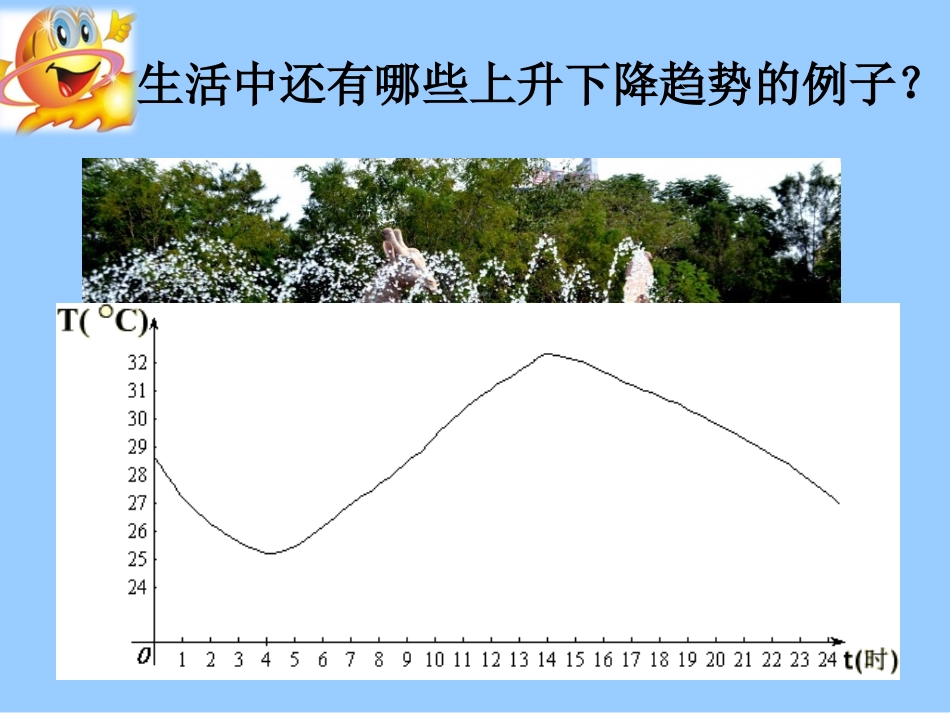
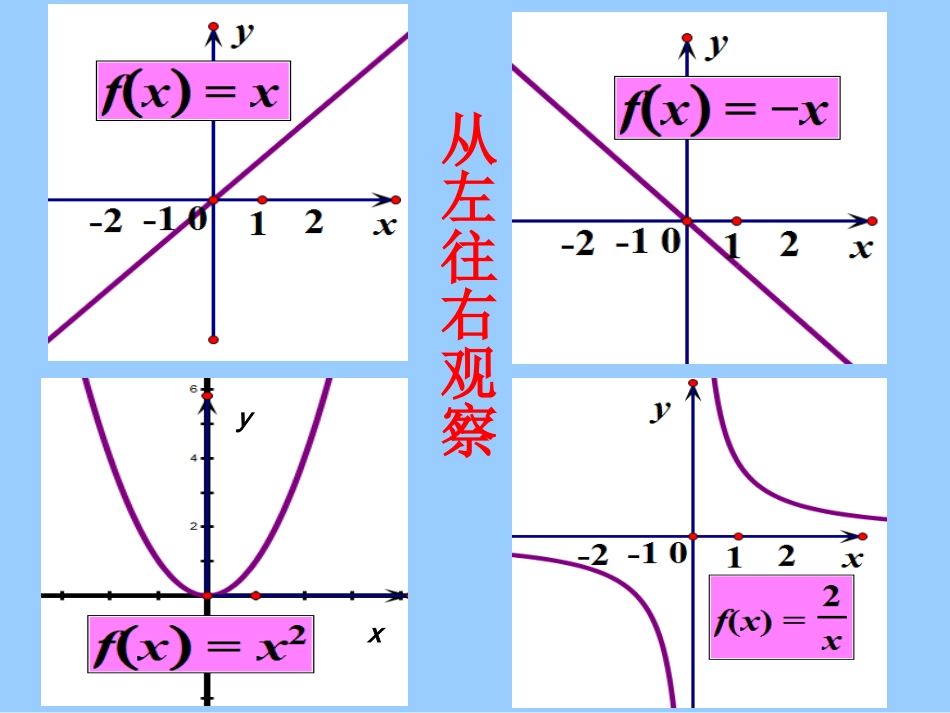
生活中还有哪些上升下降趋势的例子？xy从左往右观察函数单调性增函数的概念：一般地，函数f(x)的定义域为I：1.如果对于属于定义域内某个区间D上的任意两个称函数f(x)在这个区间上是增函数.都有时,x当x,x,x2121自变量的值21xfxfOxy)x(fy)(1xf1x)x(f22x)x(f1)x(f2)x(fyOxy1x2x上是减函数在区间那么就说函数时，都有当自变量的值上的任意两个区间如果对于定义域内某个DxfxfxfxxxxD)(),()(,,212121如果函数y=f(x)在区间D上是增函数或减函数，那么就说函数y=f(x)在这一区间具有（严格的）单调性，区间D叫做y=f(x)的单调区间。再理解：y=f(x)在D上是增（减）函数，则区间D是增（减）区间概念辨析：判断下列说法是否正确．.]2,1[)()2()1(,2,1)(2.)1(22上单调递增在那么１由于中）在函数（是减函数函数xfffxxfxy上增函数．在函数Rxf1)()3(判断单调性的方法：（1）定义（2）图象考考同桌的你：（1）自己写出一个函数，让同桌写出其增区间或者减区间。典型例题例1．如图是定义在闭区间[-5，5]上的函数y=f(x)的图象，根据图象说出y=f(x)的单调区间，以及在每一单调区间上，函数y=f(x)是增函数还是减函数.探究3:分小组画图探究下列函数的单调性，并写出其单调区间:22)(,12)(.1xxgxxf12)(,32)(.322xxxgxxxfxxgxxf4)(,4)(.2上单调递减．在定义域）当（上单调递增；在定义域）当（的单调性：一次函数RxfkRxfkkbkxxf)(,02)(,01)0()(.1结论：）上单调递增．，和（在）当（）上单调递减；，和（在）当（的单调性：反比例函数0)0,()(,020)0,()(,01)0()(.2xfkxfkkxkxf）上单调递减．，在（上单调递增，在）当（）上单调递增；，在（上单调递减，在）当（的单调性：二次函数ababxfaababxfaacbxaxxf2)2,()(,022)2,()(,01)0()(.32结论：练一练：.3,134,220,2132)(.12））（－（）；）（（）；）（－（：在下列区间上的单调性判断函数xxxf.,]2,(,),2[52)(.22的取值范围求上递减在上递增在若mmxxxf课堂小结：（1）通过增（减）函数的形成过程，你学习到了什么？（2）通过对一次函数、二次函数、反比例函数单调性的探究，你学习到了什么？