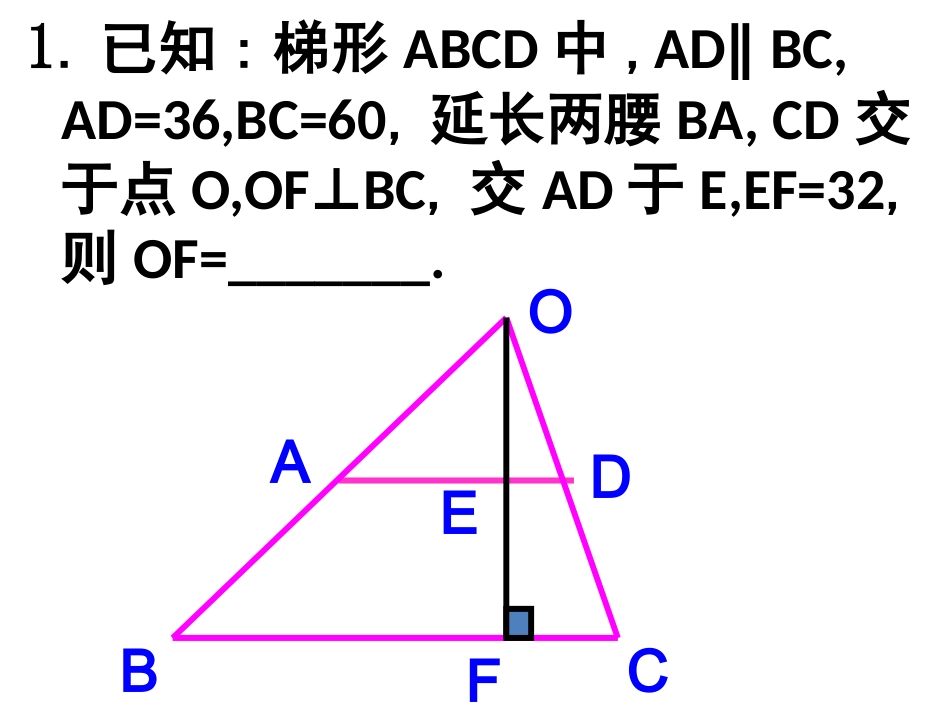
23.3.4相似三角形的应用我们已经学习相似三角形的性质有些?1.相似三角形对应角相等。2.相似三角形对应边成比例。3.相似三角形的周长之比等于相似比;4、相似三角形的面积之比等于相似比的平方。5、相似三角形的对应高线、中线、角平分线之比等于相似比。1.已知:梯形ABCD中,AD∥BC,AD=36,BC=60,延长两腰BA,CD交于点O,OFBC⊥,交AD于E,EF=32,则OF=_______.ABCDEFO2.某一时刻树的影长为8米,同一时刻身高为1.5米的人的影长为3米,则树高为.4米校园里有一棵大铁树,要测量树的高度,你有什么方法?把长为2.40m的标杆CD直立在地面上,量出树的影长为2.80m,标杆的影长为1.47m。这时树高多少?你能解决这个问题吗?(精确到0.1m)ABCDEF古代一位数学家想出了一种测量金字塔高度的方法:如图所示,为了测量金字塔的高度OB,先竖一根已知长度的木棒O′B′,比较棒子的影长A′B′与金字塔的影长AB,即可近似算出金字塔的高度OB.如果O′B′=1,A′B′=2,AB=274,求金字塔的高度OB.ABOO′B′A′步枪在瞄准时的示意图如图,从眼睛到准星的距离OE为80cm,步枪上准星宽度AB为2cm,目标的正面宽度CD为50cm,求眼睛到目标的距离OF。EABOCDF准星AB1.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.CEADBC2.为了测量一池塘的宽AB,在岸边找到了一点C,使AC⊥AB,在AC上找到一点D,在BC上找到一点E,使ED⊥AC,测出AD=35m,DC=35m,DE=30m,那么你能算出池塘的宽AB吗?ABCDE3.如图,屋架跨度的一半OP=5m,高度OQ=2.25m,现要在屋顶上开一个天窗,天窗高度AC=1.20m,AB在水平位置.求AB的长度(结果保留到0.01m)。解:由题意得,ABPO∥∴∠ABC=OPQ∠∵∠CAB=POQ=Rt∠∠∴△ABCOPQ∽△∴AB/OP=AC/OQ∴AB=OP×AC/OQ=5×1.2/2.25≈2.67m答:AB的长约为2.67m。POQABC4.如图,△ABC中,DE∥FG∥BC,AD=DF=FB,则SADE△:S四边形DFGE:S四边形FBCG=____ABCDEFG5.如图,铁道口的栏杆短臂长1m,长臂长16m,当短臂端点下降0.5m时,长臂端点升高m。OBDCA┏┛6.铁道的栏杆的短臂为OA=1米,长臂OB=10米,短臂端下降AC=0.6米,则长臂端上升BD=米。AODBC67.如图:小明在打网球时,要使球恰好能打过网,而且落在离网5米的位置上,则拍击球的高度应为()。5m10m0.9mhA、2.7米B、1.8米C、0.9米D、6米8.如图,已知零件的外径为a,要求它的厚度x,需先求出内孔的直径AB,现用一个交叉卡钳(两条尺长AC和BD相等)去量,若OA:OC=OB:OD=n,且量得CD=b,求厚度x。O(分析:如图,要想求厚度x,根据条件可知,首先得求出内孔直径AB。而在图中可构造出相似形,通过相似形的性质,从而求出AB的长度。)解:∴△AOBCOD∽△∵AB=CD·n=nb又∵CD=b且∠AOB=COD∠∵OA:OC=OB:OD=n∵OA:OC=AB:CD=n又∵x=(a-AB)÷2=(a-nb)÷2ACDbOxB9.如图,某同学拿桌刻度尺站在距电线杆30m的位置,把手臂向前伸直,把尺子竖直,看到尺子遮住电线杆时尺子刻度为12cm,已知臂长为60cm,求电线杆的高度电线杆ABCDOE10.一个高0.8m的油桶内有油,将长为1m的木棒斜插入桶内,一端到桶底,另一端在桶口,抽出木棒,量得棒上浸油部分长0.8m,求桶内有的高度?ABCDE11.如图,有一路灯杆AB,在灯光下,小明在D处的影长DE=3m,沿BD向前走5m到G点,这时小明影长GH=5m.如果小明身高为1.7m,求路灯杆AB的高度(精确到0.1m)ABDGEHCF....ABcA′B′c′1、旗杆的高度是线段;旗杆的高度与它的影长组成什么三角形?()这个三角形有没有哪条边可以直接测量?温馨提示:BC△ABC6m2、人的高度与它的影长组成什么三角形?()这个三角形有没有哪条边可以直接测量?△A′B′C′3、△ABC与△A′B′C′有什么关系?试说明理由.1.2m1.6m