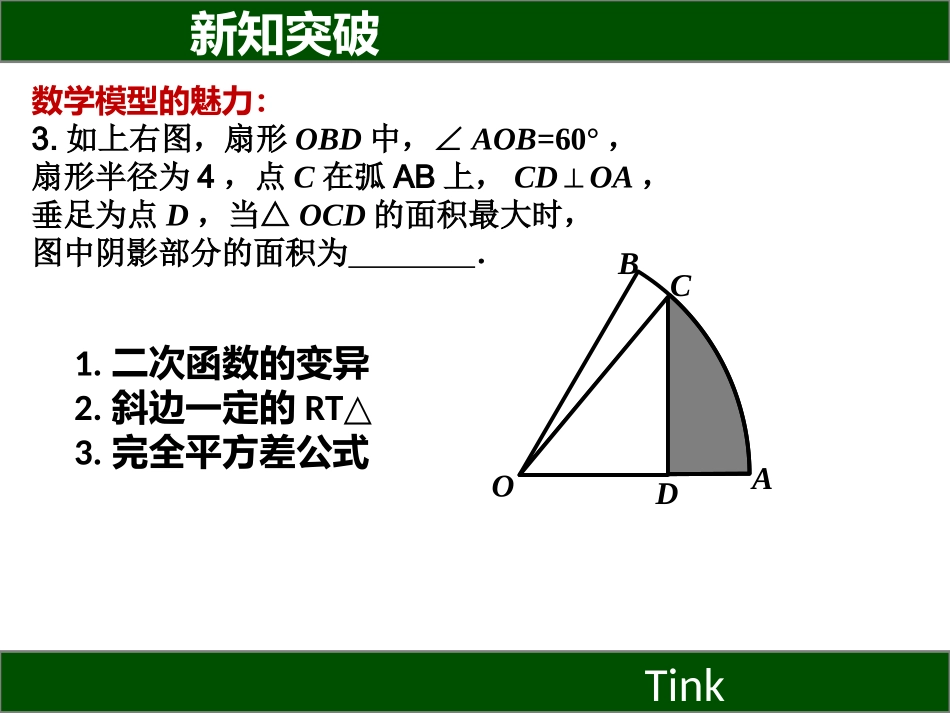
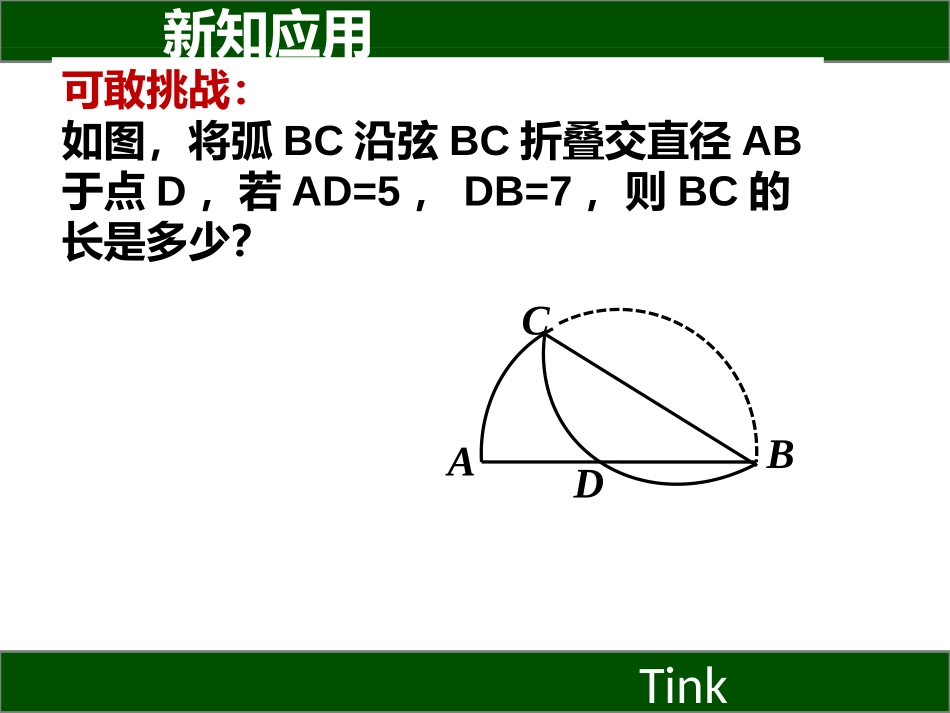
新知突破Tink数学模型的魅力:3.如上右图,扇形OBD中,∠AOB=60°,扇形半径为4,点C在弧AB上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为.AOBCD1.二次函数的变异2.斜边一定的RT△3.完全平方差公式新知应用Tink可敢挑战:如图,将弧BC沿弦BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是多少?ABDC圆的滚动专题训练1.如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为________ABCDxy例1如图所示,在直角坐标系中放置一个边长Rt△ABC,已知∠A=300,∠C=900,BC=1,将沿Rt△ABC沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为________.变式训练ABCxy将半径为2cm的圆形纸板,沿着边长分别为16cm和12cm的矩形的外侧滚动一周并回到开始的位置,圆心所经过的路线长度是____,圆滚动的圈数是____.2.中考链接O●变式:如果圆开纸板贴着矩形内侧滚动一周并回到开始的位置,圆心所经过的路线长度是____,圆滚动的圈数是____.ABCD练习:1.一位小朋友在粗糙不打滑的“Z”形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中,AB=60cm,CD=40cm,BC=40cm,请你画出圆盘从A点滚动到D点其圆心所经过的路线的示意图,并求出此路线的长度。60°BACDO60cm40cm40cm●O●●●●2.(2014•内江)通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为.O1O2O3OO′O4O5123(2009•泸州)棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积为()棱长是1cm的小立方体组成如图所示的几何体,那么这个几何体的表面积为()