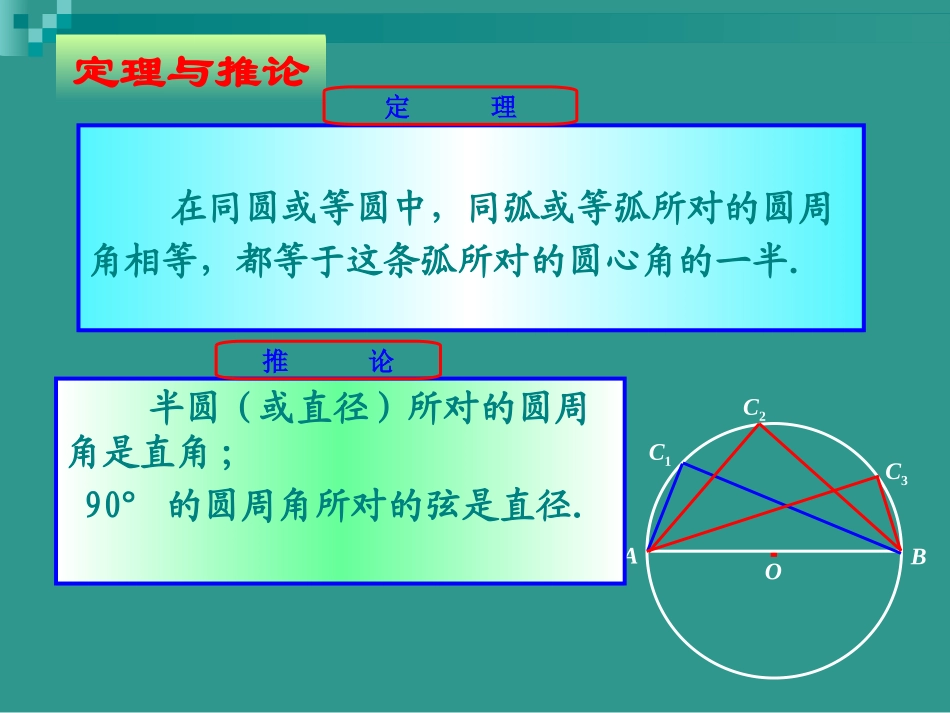
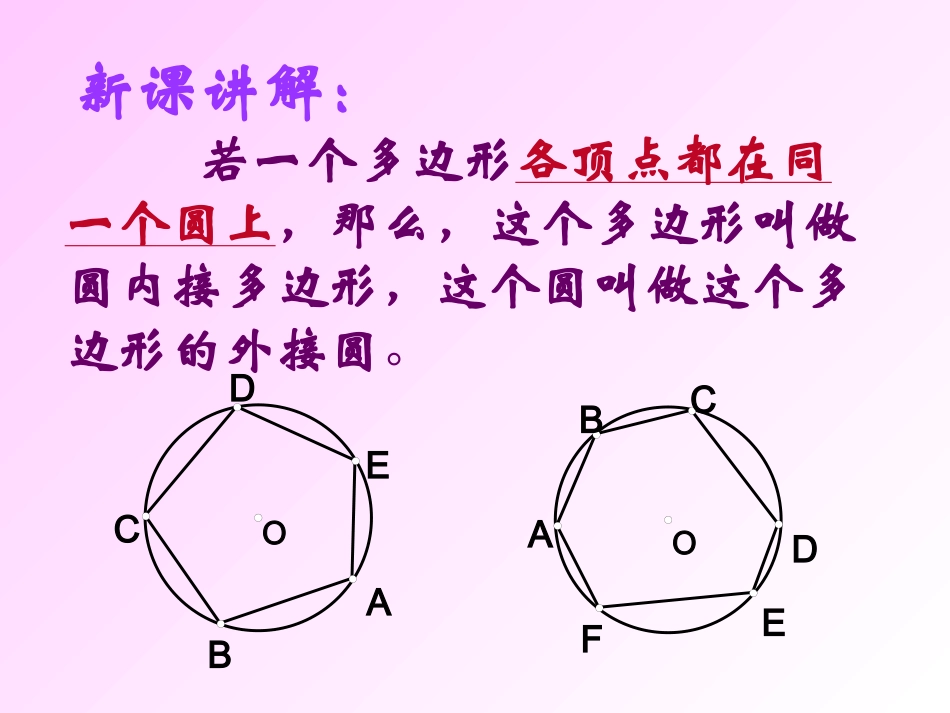
24.1.4圆周角(2)·ABC1OC2C3定理与推论在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.定理半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.推论新课讲解:若一个多边形各顶点都在同一个圆上,那么,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。OBCDEFAOACDEBOCABD如图,四边形ABCD为⊙O的内接四边形;⊙O为四边形ABCD的外接圆。思考:∠A与∠C有什么关系?∠B与∠D有什么关系?CODBA如图:圆内接四边形ABCD中,∵弧BCD和弧BAD所对的圆心角的和是周角∴∠A+∠C=180°同理∠B+∠D=180°圆的内接四边形的对角互补。如果延长BC到E,那么∠DCE与∠A有什么关系?所以∠A=∠DCE又∠A+∠BCD=180°CODBAE∠DCE+∠BCD=180°要会用到解题中•定理:圆的内接四边形的对角互补。几何表达式:∵ABCD是⊙O的内接四边形,∴∠A+∠C=180°DABC1E(1)四边形ABCD内接于⊙O,则∠A+C=______B+ADC=_______;∠∠∠若∠B=80°,则∠ADC=____CDE=______∠(2)四边形ABCD内接于⊙O,∠AOC=100°则∠B=______D=______∠(3)四边形ABCD内接于⊙O,A:C=1:3,∠∠则∠A=_____,180°180°100°80°50°130°45°EDBAC80DBACO100(4)梯形ABCD内接于⊙O,AD∥BC,∠B=750,则∠C=_____75°返回圆的内接梯形一定是_____梯形。DBACO例如图,⊙O直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,求BC、AD、BD的长.86102222ACABBC又在Rt△ABD中,AD2+BD2=AB2,221052(cm)22ADBDAB解:∵AB是直径,∴∠ACB=∠ADB=90°.在Rt△ABC中,∵CD平分∠ACB,∴AD=BD..ACDBCD例题OABCD例如图⊙O1与⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2交于点D。经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F。求证:CE∥DF12OOFABECD12OOFABECDCE∥DF1∠E+∠F=180°∠E+∠1=180°、∠1=∠FABEC是⊙O1的内接四边形ABFD是⊙O2的内接四边形连结AB证明:连结AB∵ABEC是⊙O1的内接四边形,∴∠1=∠F∵ADFB是⊙O2的内接四边形,∴∠E+∠1=180°∴∠E+∠F=180°∴CE∥DF12OOFABECD112OOFABECDGH反思与拓展证明两条直线平行的方法很多,但常用的还是通过证明同位角相等、内错角相等、同旁内角互补等方法。刚才我们通过同旁内角互补证明了CE∥DF,想一想还能否通过同位角相等或者内错角相等证明结果?1)延长EF,是否有∠E=BAD∠=∠1?AO21O1BCDEFM2)延长DF,能否证明∠E=∠2=∠3?A2O23O1BCDEFO1BO2ACDEF1巩固练习:1、如图,四边形ABCD为⊙O的内接四边形,已知∠BOD=100°,求∠BAD及∠BCD的度数。AODBC2.求证:圆内接平行四边形是矩形。OCDBA3.已知:如图,四边形ABCD是圆的内接四边形并且ABCD是平行四边形。求证:四边形ABCD是矩形。(1)如图5,四边形ABCD内接于⊙O,则∠A+∠C=__,∠B+∠ADC=_____;若∠B=800,则∠ADC=______∠CDE=______(2)如图6,四边形ABCD内接于⊙O,∠AOC=1000则∠B=______∠D=______(3)四边形ABCD内接于⊙O,∠A:∠C=1:3,则∠A=_____,EDBAC80DBACO100180°180°100°80°50°130°45°4.填空图5图6)(DBACO(4)梯形ABCD内接于⊙O,AD∥BC,∠B=750,则∠C=_____75°圆的内接梯形一定是_____梯形。等腰若ABCD为圆内接四边形,则下列哪个选项可能成立()(A)∠ABCD∠∠∠=1234∶∶∶(B)∠ABCD∶∠∶∠∶∠=2134∶∶∶(C)∠ABCD∶∠∶∠∶∠=3214∶∶∶(D)∠ABCD∶∠∶∠∶∠=4321∶∶∶B补充练习:布置作业:教科书86页A组15、16、17题;B组1、5题因为∠A是与∠DCE相邻的内角∠DCB的对角,我们把∠A叫做∠DCE的内对角。圆内接四边形的一个外角等于它的内对角。CODBAECODBAE1234567定理:圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角。要会背,你会背了吗?