椭圆及其标准方程VIP免费

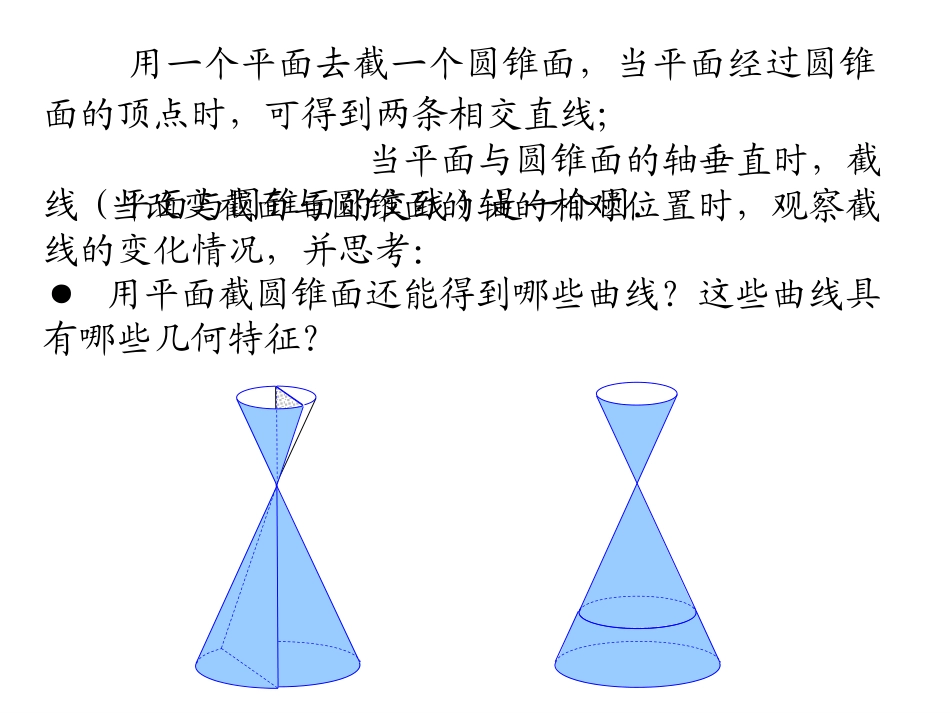
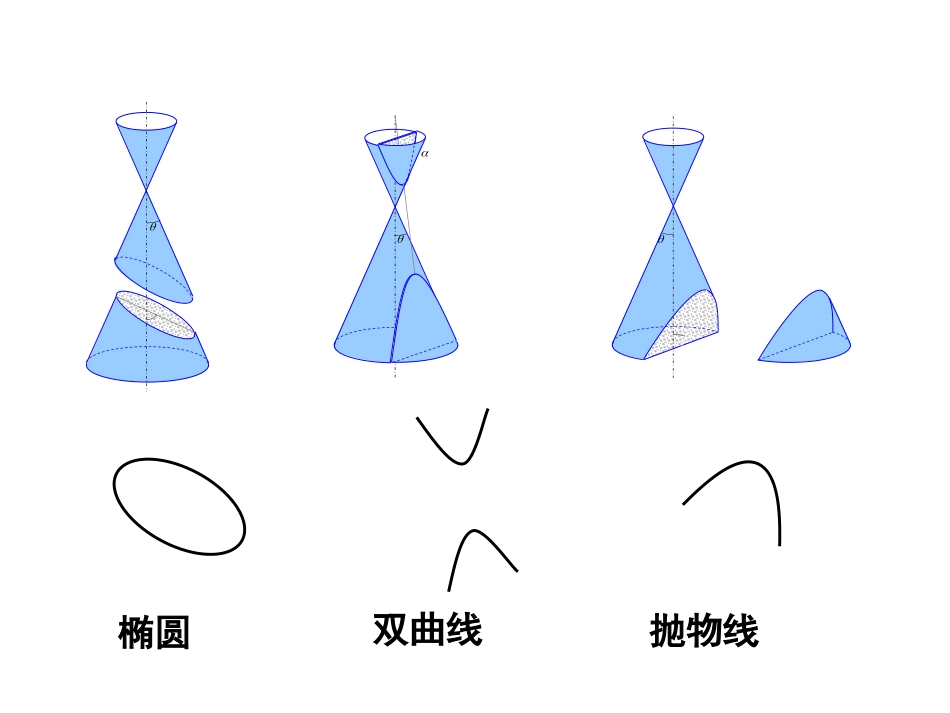
用一个平面去截一个圆锥面，当平面经过圆锥面的顶点时，可得到两条相交直线；当平面与圆锥面的轴垂直时，截线（平面与圆锥面的交线）是一个圆．当改变截面与圆锥面的轴的相对位置时，观察截线的变化情况，并思考：●用平面截圆锥面还能得到哪些曲线？这些曲线具有哪些几何特征？椭圆双曲线抛物线1F2FM112.图?,?,,,),.(,.,,,,,足的几何条件吗满动点你能说出移动笔尖在这一过程中曲线画出的轨迹是什么移动笔尖拉紧绳子上铅笔套图处分别固定在图板的两点段距离一如果把细绳的两端拉开画出的轨迹是一个圆动点这时笔尖动笔尖移拉紧绳子套上铅笔定在图板的同一点处把它的两端都固细绳的长条定取一究探112绘图纸上的三个问题1．视笔尖为动点，两个图钉为定点，动点到两定点距离之和符合什么条件？其轨迹如何？2．改变两图钉之间的距离，使其与绳长相等，画出的图形还是椭圆吗？3．绳长能小于两图钉之间的距离吗？归纳：椭圆的定义：平面内与两定点F1、F2的距离之和等定长（大于|F1F2|）的点的轨迹叫椭圆.定点F1、F2叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距.探究结论探究结论：：若常数若常数大于大于|F|F11FF22|,|,则点则点MM的轨迹是（）的轨迹是（）若常数若常数等于等于|F|F11FF22||，则点，则点MM的轨迹是（）的轨迹是（）若常数若常数小于小于|F|F11FF22||，则点，则点MM的轨迹（）的轨迹（）椭圆椭圆线段线段FF11FF22不存在不存在1F2FM取一条定长的细绳,把两端拉开一段距离分别固定在图板的两点处，套上铅笔，拉紧绳子，移动笔尖，画出的是什么图形？该曲线满足的条件是什么？12PMMFMF定值1F2FM平面内与两定点的距离之和等于常数的点的轨迹叫做椭圆。)(21FF大于这两个定点叫做椭圆的焦点两焦点间的距离叫做椭圆的焦距1F2FM（3）由定有________________________,由距离公式有__________________________列式：____,0c（）,0c（）,xy2FM1Fxyo2222x+cx-c2yya（）（）（2）设点：设M(x,y)是椭圆上任意一点，焦距为2c(c>0),那么焦点F1，F2的坐标分别是，设M与焦点F1，F2的距离的和为（其中），2aac12PMMFMF定值以椭圆两焦点F1，F2所在的直线为X轴，线段F1F2的垂直平分线为Y轴（-c，0），（c，0）1（）建系：______________________________________________________,建立直角坐标系。1F2FM22x+c_______________(__;4)y：移项：（）化简222x-cay（）222222244xcx+cxcaayyy（）（）方程两边平方:（）22x_______c____ay（）整理移项:2222222422222axacxacayaacxcx上式两边再平方，得:222()()ya整理得:（）x22222___________1yaacx两边同除以，得2222222222,0,1(0)acacacybacabab由2即，所以x令，则22ac2a22ac222aac（）2acxy2.若焦点在轴上，类似的求出椭圆方程为___________22221yabx思考1、对于椭圆的标准方程中的两个字母及，①结合“下图与椭圆方程的推导过程”，指出分别指的哪条线段；②它们之间的数量关系是。22221(0)xyabab,abc,,abc1212,,aPFPFbOPcOFOF222abcjF2F1POxy不同点标准方程图形焦点坐标共同点定义a、b、c的关系焦点位置的判定1,0Fc2,0Fc222(0,0)abcabc10,Fc20,Fc焦点在大数对应的轴上22221(0)xyabab22221(0)yxabab2FM1FxyM2Fxy1F1222MFMFaac（2）尝试练习一：1、在下列方程中，哪些是椭圆的标准方程？如果是，请找出a,b,c的值.22222222(1)0(2)1254169(3)1(4)125429xyxyxyxy2、根据椭圆的方程填空22(1)110036xyabc则焦点坐标abc则焦点坐标22(2)158xy106(8,0),(8,0)8225(0,3),(0,3)3abc则焦点坐标22(3)4936xy325(5,0),(5,0)例2、已知方程表示椭圆，则当实数k取何值时，方程表示：⑴焦点在x轴的椭圆，⑵焦点在y轴的椭圆221159xykk例题分析：例1已知椭圆两个焦点的坐标分别是（-2，0），（2，0），并且经过点求它的标准方程。53,,22例2.已知...